Lokale Extremstellen

Viele Aufgabenstellungen sind mit der Suche nach Hoch- und Tiefpunkten verbunden. Graphisch fällt es ziemlich leicht, die gesuchten Punkte zu finden.

Dank der Ableitungen von Funktionen ist es auch möglich, die gesuchten Stellen zu finden, ohne den Graphen zeichnen zu müssen, verbunden mit der Tatsache, dass die gefundenen Werte exakter sind, da die Stellen nicht abgeschätzt werden, sondern berechnet werden können.

Im folgenden betrachten wir zwei Möglichkeiten, lokale Extremstellen zu finden, wobei die untersuchten Funktionen mehrfach differenzierbar sein sollen (also ableitbar und damit "ohne Knick") und jede Funktion und ihre Ableitungen stetig, also "in einem Zug zeichenbar".

Das Besondere an Hoch- und Tiefpunkten ist zum einen, dass dort waagrechte Tangenten vorliegen.

Somit ist die erste Ableitung der Funktion \$f\$ an dieser Stelle 0.

Aber Vorsicht:

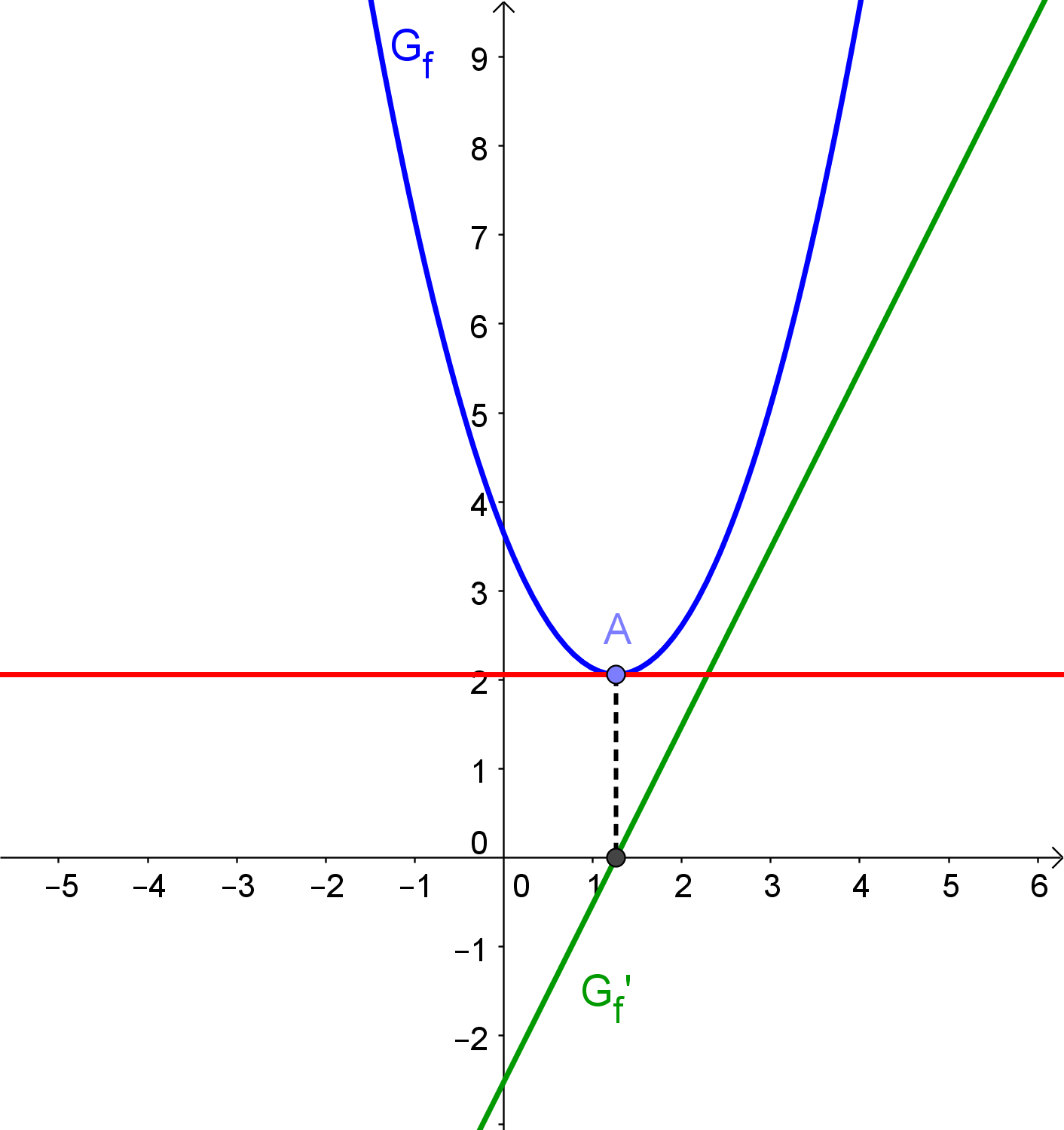
Ein einfaches Gegenbeispiel ist eine Funktion dritten Grades, die einen Sattelpunkt aufweist. In diesem Fall ist die erste Ableitung an dieser Stelle zwar 0, eine Extremstelle liegt hier aber nicht vor:

Somit ist die Tatsache, dass \$f'(x_0)=0\$ sein muss zwar notwendig, aber nicht hinreichend für die Existenz einer Extremstelle von \$f\$ bei \$x_0\$.

Vergleicht man die Schaubilder der ersten Ableitung für den Fall der Extremstelle und für den Sattelpunkt, so fällt auf, dass im Fall der Extremstelle die erste Ableitung dort 0 ist und einen Vorzeichenwechsel aufweist.

Im Fall des Sattelpunktes ist die erste Ableitung dort zwar 0, wechselt aber nicht ihr Vorzeichen.

Somit können wir also auf die Existenz einer Extremstelle an einer Stelle \$x_0\$ schließen, wenn \$f'(x_0)=0\$ ist und zum anderen der Graph von \$f'\$ bei \$x_0\$ einen Vorzeichenwechsel hat.

Somit formulieren wir die

Durch die erste hinreichende Bedingung haben wir bereits ein Werkzeug, das uns das Auffinden von Extremstellen vereinfacht. In diesem Abschnitt werden wir noch eine weitere Möglichkeit kennenlernen, diese rechnerisch zu bestimmen.

Dazu betrachten wir die gleichen Beispiele wie im letzten Abschnitt, nur beziehen wir in unsere Betrachtung noch die zweite Ableitung mit ein.

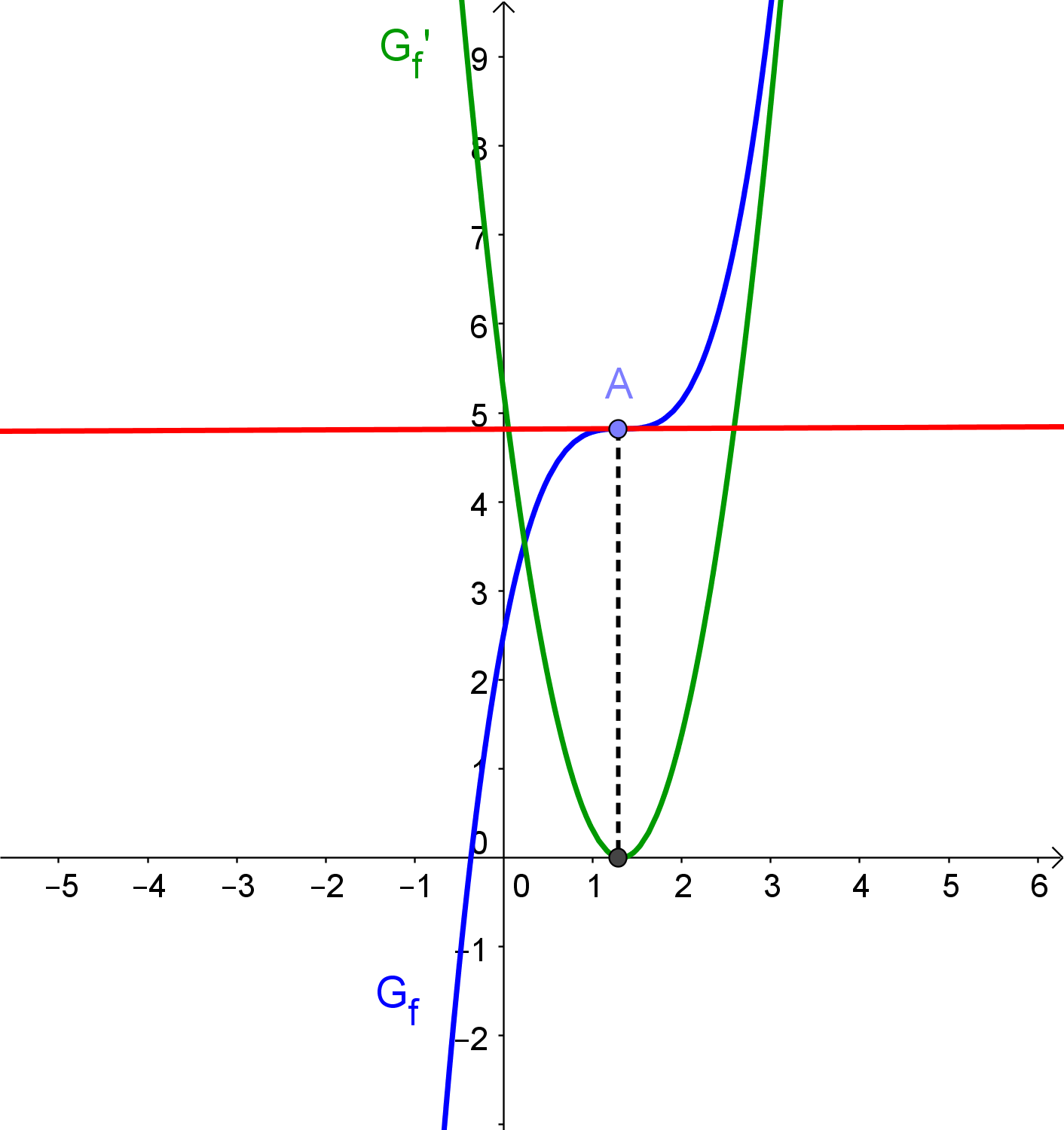
Zunächst untersuchen wir wieder die nach oben geöffnete Parabel:

Da der Graph von \$f\$ im Bereich seines Minimums eine Linkskurve beschreibt, ist \$f''\$ in diesem Bereich positiv. Bei einem Maximum läge eine Rechtskurve vor, so dass \$f''\$ in diesem Bereich negativ wäre.

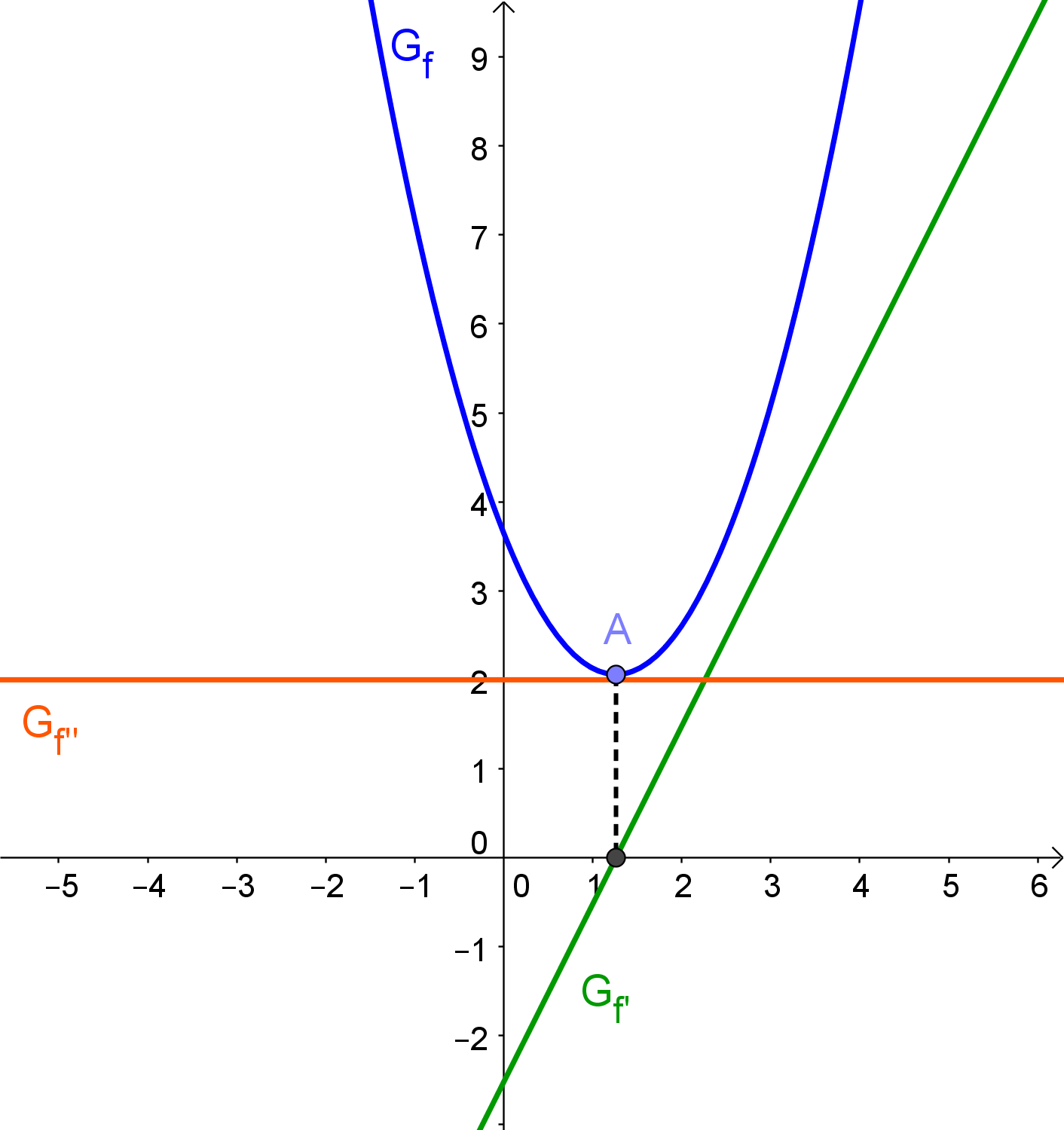
Im Falle eines Sattelpunktes ergibt sich die folgende Situation:

Man sieht: da an dieser Stelle weder eine Links- noch eine Rechtskurve im Graphen von \$f\$ vorliegt, ist die zweite Ableitung an dieser Stelle 0.

Somit formulieren wir

In vielen Fällen scheint die zweite hinreichende Bedingung (mit der zweiten Ableitung) zunächst das einfachere Kriterium zu sein. Man beachte aber das folgende Beispiel:

Bestimmung der Extremstellen mit Hilfe der zweiten hinreichenden Bedingung:

Weiter gilt, dass \$f'(0)=0\$ und \$f''(0)=0\$. Somit ist nach der zweiten hinreichenden Bedingung zunächst keine Aussage möglich. Vielmehr liegt die Vermutung nahe, dass es sich hier um eine Sattelstelle handelt.

Versucht man jedoch, die erste hinreichende Bedingung anzuwenden, so ergibt die Überprüfung auf einen Vorzeichenwechsel bei \$x_0=0\$

Bei 0 liegt somit ein Vorzeichenwechsel von - nach + vor, so dass dort nach der ersten hinreichenden Bedingung eine Minimumstelle vorliegen muss.

Ein Sonderfall in Bezug auf lokale Extremstellen ist eine konstante Funktion der Form \$f(x)=c\$ mit \$c in RR\$.

Sie hat nach Definition unendlich viele lokale Maxima bzw. Minima. Das liegt daran, dass z. B. eine lokale Minimumstelle definiert ist als eine Stelle \$x_0\$, für die gilt \$f(x)>=f(x_0)\$ für alle \$x in U(x_0)\$, wobei mit \$U(x_0)\$ die nähere Umgebung von \$x_0\$ gemeint ist.

Da ein Kleiner-Gleich-Symbol in der Definition vorliegt, erfüllt eine konstante Funktion an jeder Stelle diese Voraussetzung, besitzt also an jeder Stelle ein lokales Minimum.

Analog dazu hat die Funktion auch an jeder Stelle ein lokales Maximum.

Überprüfen wir diese Eigenschaft mit Hilfe der hinreichenden Bedingungen so erhält man für \$f(x)=c\$ als erste Ableitung \$f'(x)=0\$ und als zweite Ableitung ebenfalls \$f''(x)=0\$.

Die zweite hinreichende Bedingung ist nirgendwo auf dem Definitionsbereich erfüllt, da die zweite Ableitung nirgendwo ungleich 0 ist und somit keine Aussage getroffen werden kann.

Die erste hinreichende Bedingung kann für die erste Ableitung nirgendwo einen Vorzeichenwechsel vorfinden und somit auch keine Aussage über das Vorliegen von Extremstellen treffen.

Dies ist also ein Beispiel, in dem weder die erste noch die zweite hinreichende Bedingung die Extremstellen auffinden kann.

Somit gilt:

Aufgabe:

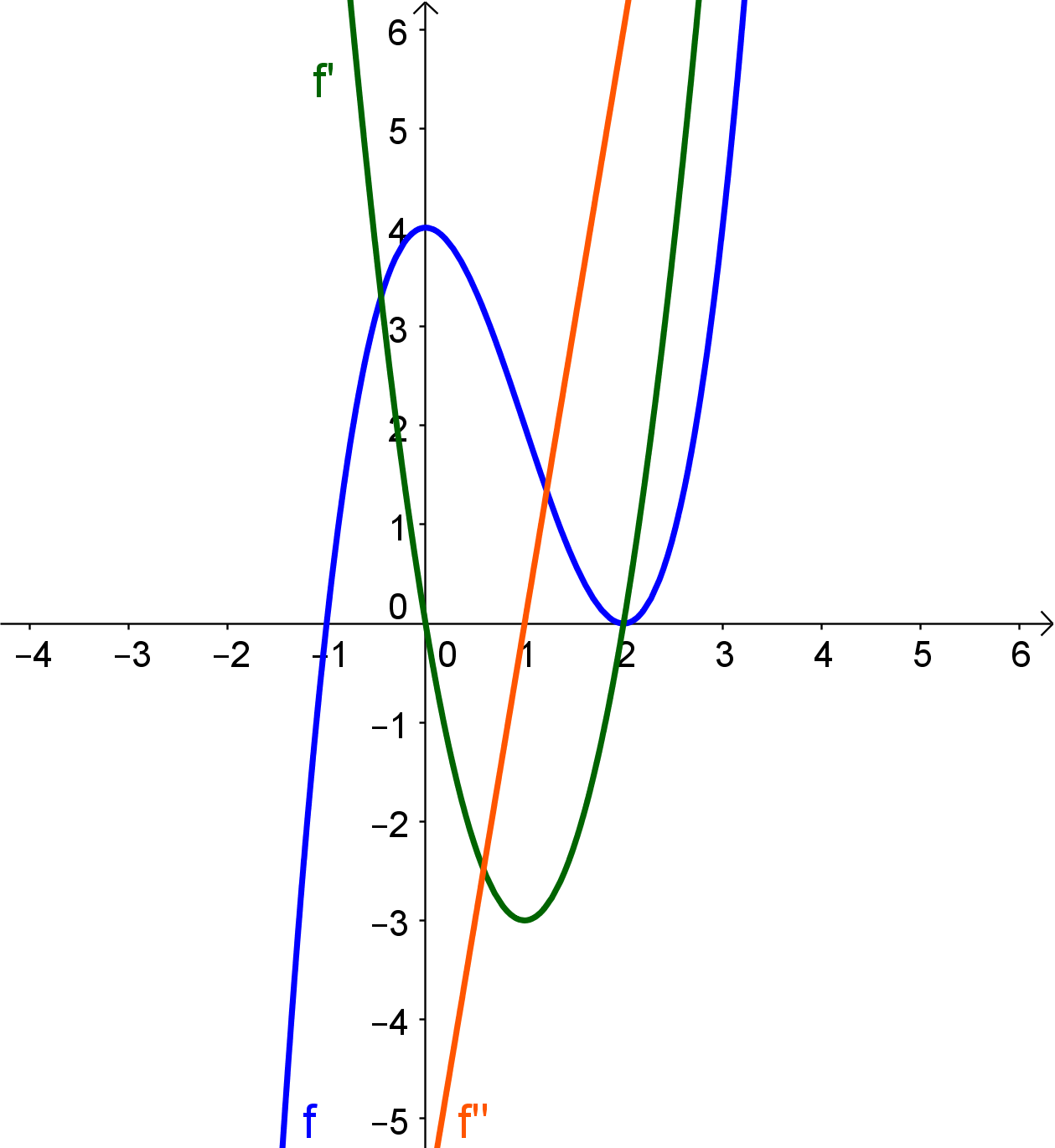
Gegeben sei \$f(x)=x^{3} - 3 x^{2} + 4\$. Bestimme die Extrempunkte dieser Funktion a) mit der ersten hinreichenden Bedingung und b) mit der zweiten hinreichenden Bedingung.

Lösung:

Zunächst bestimmen wir für diese Aufgabe die nötigen Ableitungen:

\$f'(x)=3x^2-6x\$ und \$f''(x)=6x-6\$.

Für beide hinreichenden Bedinungen benötigen wir die Stellen, an denen \$f'(x)=0\$ ist, also setzen wir an:

\$3x^2-6x=0\$

Ausklammern von x liefert:

\$x*(3x-6)=0\$

Mit Hilfe des Satzes des Nullprodukts sieht man, dass eine Nullstelle von \$f\$ an der Stelle \$x_1=0\$ vorliegt. Die zweite Möglichkeit, dass die erste Ableitung 0 wird, liegt vor, wenn \$3x-6=0\$, also wenn \$x_2=2\$ ist.

Somit sind \$x_1=0\$ und \$x_2=2\$ Kandidaten für Extremstellen von \$f\$.

Nun überprüfen wir mit den hinreichenden Bedingungen, ob hier tatsächlich Extremstellen vorliegen:

Zu a)

Wir überprüfen die \$f'\$ auf Vorzeichenwechsel an den Stellen \$x_1\$=0 und \$x_2\$=2 mit Hilfe einer Tabelle:

Somit liegt bei \$x_1=0\$ ein Vorzeichenwechsel von + nach - vor, also weist f an dieser Stelle ein Maximum auf (links davon steigt der Graph, rechts davon fällt er).

Bei \$x_2=2\$ liegt ein Vorzeichenwechsel von - nach + vor, also hat f an dieser Stelle ein Minimum.

Zu b)

\$f''(x_1)=f''(0)=-6 < 0 =>\$ Rechtskurve von \$f\$, also Maximum bei \$x_0=0\$

\$f''(x_2)=f''(2)=6 > 0 =>\$ Linkskurve von \$f\$, also Minimum bei \$ x_1=2\$

Da in der Aufgabe nach den Extrempunkten gefragt ist, muss man noch den jeweiligen y-Wert bestimmen:

\$f(x_1)=f(0)=4\$ und \$f(x_2)=f(2)=0\$.

Somit liegen ein Hochpunkt H(0/4) und ein Tiefpunkt T(2/0) vor.

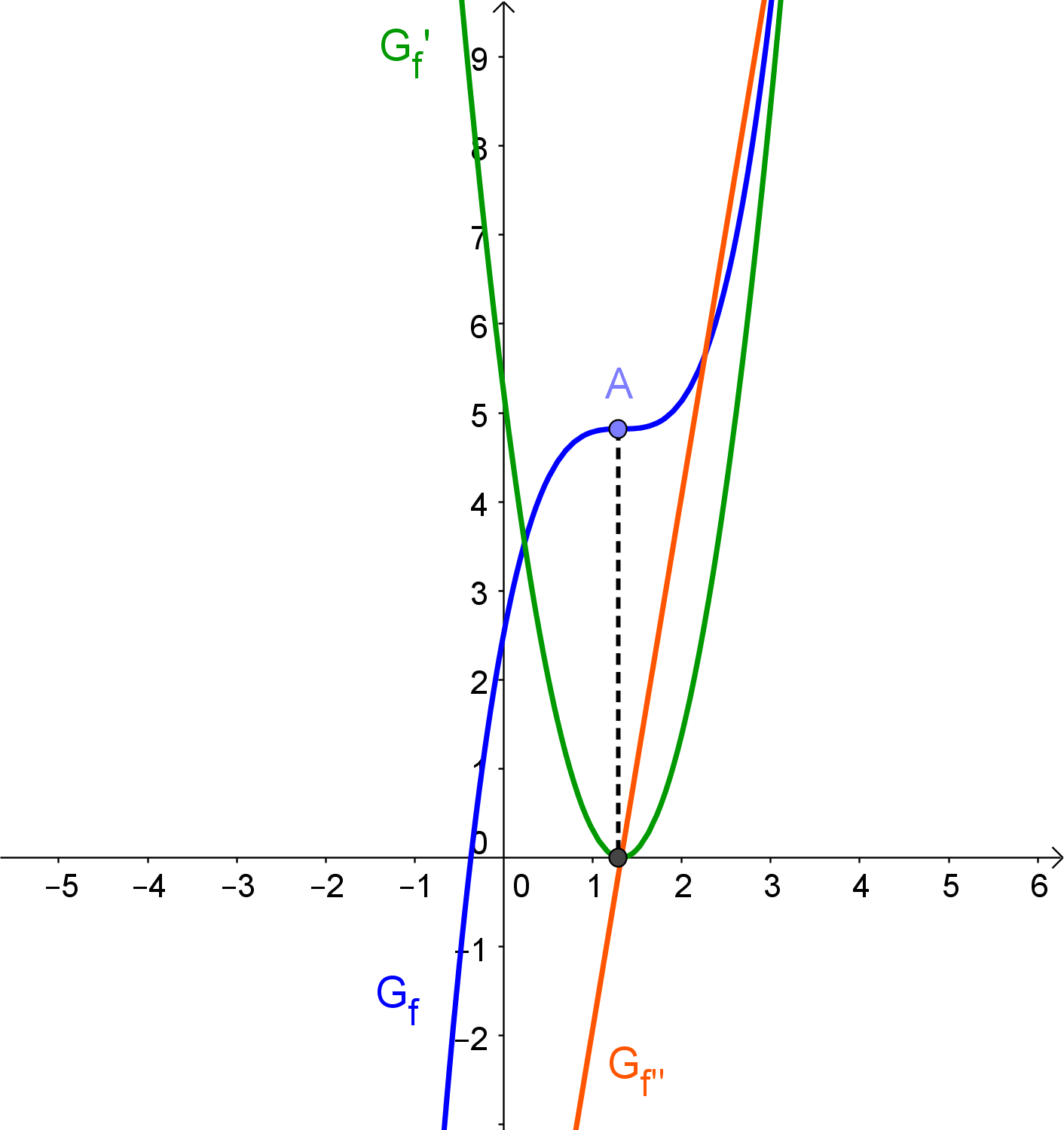
Zur Kontrolle hier das Schaubild der Funktion und der ersten beiden Ableitungen: