1. Motivation
Mit Hilfe der ersten Ableitung kann man an einem Punkt im Graph einer Funktion \$f\$ die Steigung der Tangente durch diesen Punkt berechnen. Möchte man jedoch die Gleichung der Tangente aufstellen, so muss man noch weitere Schritte unternehmen. Dieses Kapitel erklärt Vorgehensweisen, um die Gleichungen von Tangenten und Normalen durch Punkte eines Graphen zu bestimmen.
2. Begriffsklärung
Das folgende Schaubild zeigt die Tangente und die Normale an f in einem Punkt A:
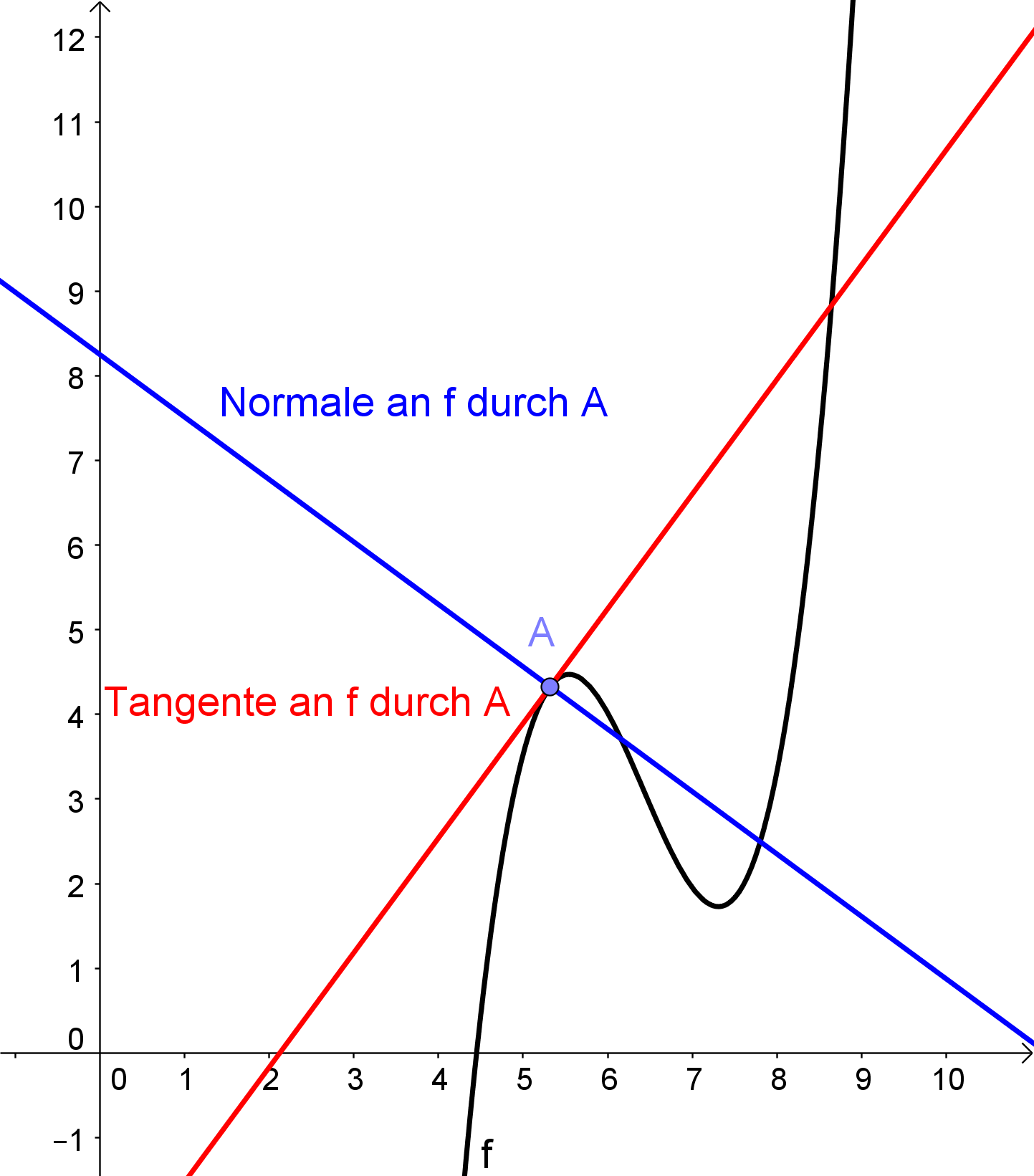
Die Tangente ist die Gerade, die in einem Punkt A des Graphen von f die gleiche Steigung hat wie der Graph selbst und durch den Punkt A verläuft, die Normale ist die Gerade durch A, die auf der Tangente senkrecht steht.
3. Die Tangentengleichung
3.1. Herleitung
Da es sich bei Tangente und Normale jeweils um Geraden handelt, können die zugehörigen Terme über die allgemeine Geradengleichung \$y=m * x+c\$ bestimmt werden.
Im Fall der Tangente an einem Punkt \$A(u|f(u))\$ ist die Steigung \$m=f'(u)\$. Somit kann man schreiben:
\$y=f'(u)*x+c\$.
Zunächst scheinen drei Variablen, nämlich \$y\$, \$x\$ und \$c\$ unbekannt zu sein. Da man aber weiß, dass der Punkt A auf der Tangente liegt, muss dieser auch die Tangentengleichung erfüllen. Dadurch kann man für \$y=f(u)\$ schreiben und für \$x=u\$. Man erhält durch dieses Einsetzen die Gleichung
\$f(u)=f'(u)*u+c\$,
wodurch ein Umformen nach \$c\$ den Ausdruck
\$c=f(u)-f'(u)*u\$
liefert.
Setzt man dieses \$c\$ und \$m=f'(u)\$ in die allgemeine Geradengleichung \$y=m * x+c\$ ein, so erhält man für den Funktionsterm der Tangente
\$t(x)=f'(u)*x+f(u)-f'(u)*u\$
und kann diesen Ausdruck über das Ausklammern von \$f'(u)\$ umformen zu
\$t(x)=f'(u)*(x-u)+f(u)\$.
Diese Gleichung heißt
Tangentengleichung:
Die Gleichung der Tangente an den Graph von \$f\$ in einem Punkt \$A(u|f(u))\$ lautet
\$t(x)=f'(u)*(x-u)+f(u)\$.
3.2. Beispiele zur Tangentengleichung
Aufgabe 1: Punkt auf dem Graphen gegeben
Gegeben sei \$f(x)=x^2\$. Bestimme die Gleichung der Tangente am Punkt \$P(3|f(3))\$.
Lösung:
Variante 1: Mit der Tangentengleichung
\$u=3\$, \$f(u)=f(3)=3^2=9\$.
\$f'(x)=2x\$, also ist \$f'(u)=f'(3)=2*3=6\$.
Einsetzen in die Tangentengleichung liefert: \$t(x)=6*(x-3)+9=6x-18+9=6x-9\$
Variante 2: Mit der normalen Geradengleichung
\$y=m*x+c\$ mit \$m=f'(3)=6\$ (s. oben). Da der Punkt \$P(3|f(3)=9)\$ auf der Tangente liegt, gilt die Gleichung
\$9=6*3+c\$.
Somit gilt: \$c=9-18=-9\$, also erhält man als Tangentengleichung \$t(x)=6x-9\$.
Aufgabe 2: Tangente von einem Punkt außerhalb des Graphen
Gegeben sei \$f(x)=x^2\$. Bestimme die Gleichung der Tangente an den Graph von \$f\$ durch den Punkt \$Q(3|1)\$ und die Punkte \$P\$, an denen die Tangente den Graph von \$f\$ berührt.
Lösung:
Der Punkt Q liegt nicht auf dem Graph von \$f\$, allerdings muss er natürlich auch die Tangentengleichung erfüllen, so dass man durch Einsetzen von \$t(x)=1\$ und \$x=3\$ die Gleichung
\$1=f'(u)*(3-u)+f(u)\$
erhält. Setzt man nun für \$f(u)=u^2\$ und für \$f'(u)=2u\$ ein, so gilt:
\$1=2u*(3-u)+u^2\$.
Diese Gleichung kann man nach kurzer Umformung mit Hilfe der Mitternachtsformel lösen:
\$1=6u-2u^2+u^2=6u-u^2\$
Standardform aufstellen, \$u^2-6u+1=0\$, und einsetzen:
\$u_{1|2}={6+-sqrt{36-4*1*1}}/2={6+-4 sqrt{2}}/2\$
ergibt \$u_1=3+2 sqrt(2)~~5,83\$ und \$u_2=3-2 sqrt(2)~~0,17\$.
Somit gibt es zwei mögliche Punkte, an denen eine Tangente durch den Punkt \$Q\$ den Graph von \$f\$ berührt, nämlich \$P_1(5,83|33,99)\$ und \$P_2(0,17|0,029)\$.
Somit lautet die Gleichung der einen Tangente
\$t_1(x)~~2*5,83*(x-5,83)+33,99=11,66*x-67,98+33,99=11,66x-33,99\$
und die der anderen analog dazu
\$t_2(x)~~2*0,17*(x-0,17)+0,029=0,34x-0,0578+0,029=0,34x-0,0288\$.
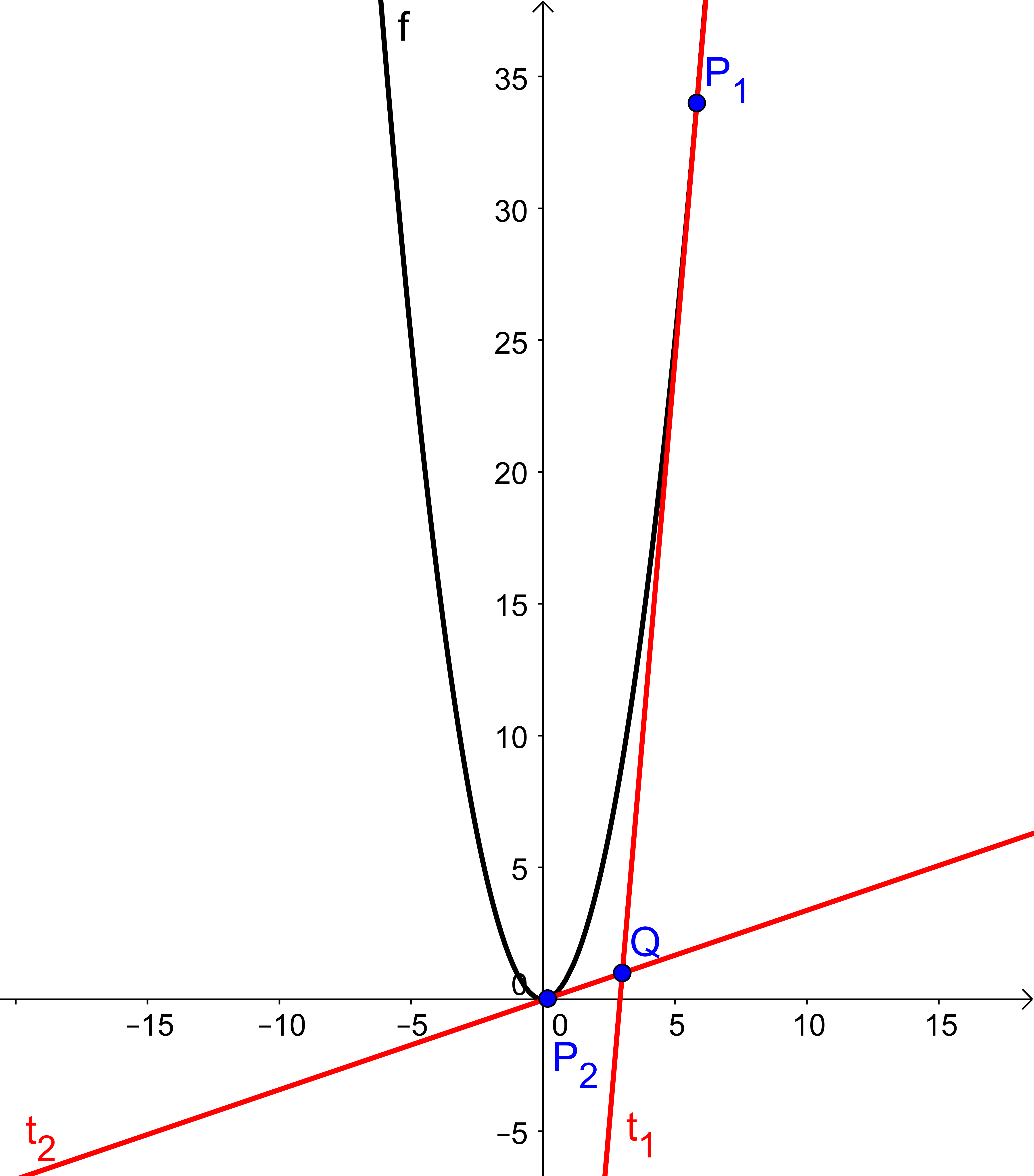
Im Schaubild sind die Lösungen nochmal visualisiert. Hier erkennt man auch, dass es tatsächlich zwei Tangenten geben muss.
4. Die Normale
4.1. Zusammenhang Tangente und Normale
Zeichnet man ein Steigungsdreieck an eine Gerade, so hat diese Gerade die Steigung \$m= {Delta y}/ {Delta x}\$, wobei \$Delta x\$ angibt, wie weit man nach rechts gehen muss, \$Delta y\$ hingegen, wie weit nach oben.
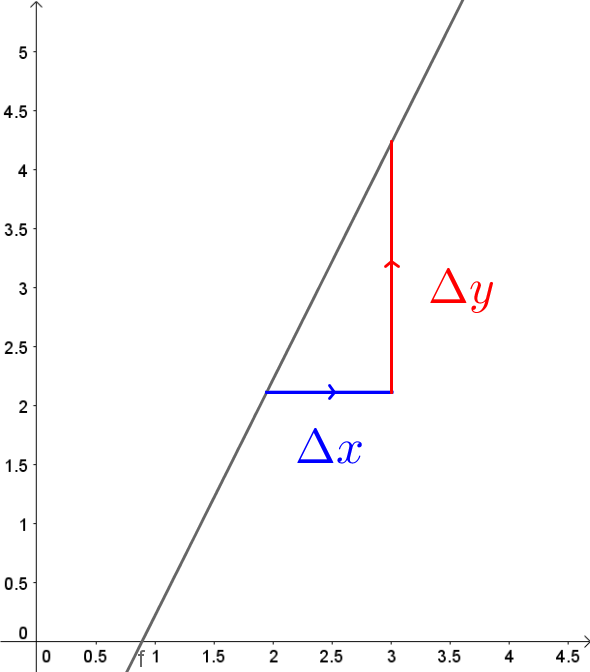
Nun drehen wir das Bild um 90 Grad und erhalten dadurch die Gerade, die auf der vorherigen senkrecht steht:
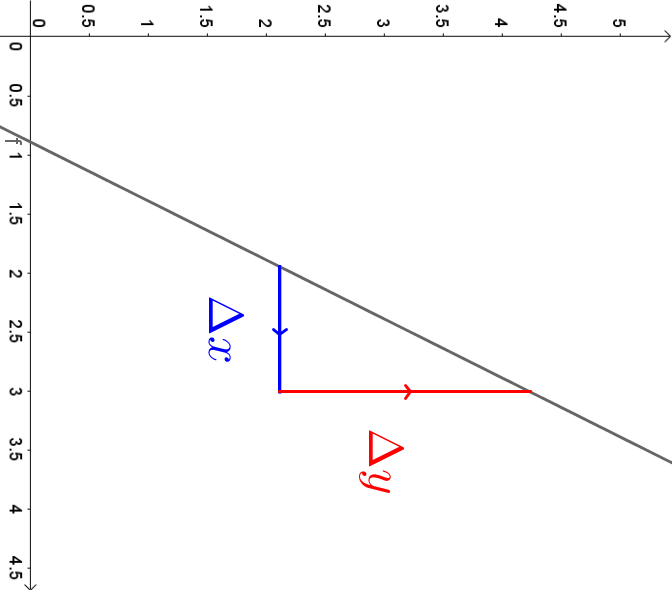
Die Steigung der neuen Gerade erhält man nun wieder über das Steigungsdreieck. Die neue Steigung ist nun allerdings
\$m_{text(neu)}={-Delta x} / { Delta y}=-{Delta x} / {Delta y}=-1/({Delta y} / {Delta x})=-1/m\$,
da man zunächst um \$Delta x\$ nach unten geht (also "um \$-Delta x\$ nach oben") und um \$Delta y\$ nach rechts.
|
Oder anders erklärt: Im Vergleich zur ersten Gerade mit der Steigung \$m= {Delta y} / {Delta x}\$ sind \$Delta x\$ und \$Delta y\$ vertauscht und da durch die Drehung aus einer positiven Steigung eine negative wird, muss man auch noch das Vorzeichen anpassen. Dadurch gilt \$m_{text(neu)}=-{Delta x} / {Delta y}\$. |
Somit gilt allgemein:
Steigungen aufeinander senkrecht stehender Geraden:
Stehen zwei Geraden mit den Steigungen \$m_1\$ und \$m_2\$ aufeinander senkrecht, so gilt:
\$m_2=- 1/m_1\$
bzw.
\$m_1 * m_2=-1\$
Wendet man diese Erkenntnis auf die Tangentengleichung an, so erhält man als
Normalengleichung:
Die Gleichung der Normale an den Graph von \$f\$ in einem Punkt \$A(u|f(u))\$ lautet
\$n(x)=- 1 / {f'(u)} *(x-u)+f(u)\$
mit \$f'(u)!=0\$.
4.2. Beispiel zur Berechnung der Normale
Aufgabe:
Berechne die Normale am Graph der Funktion \$f(x)=x^2\$ im Punkt \$P(3|f(3))\$.
Lösung:
Aus Aufgabe 1 zur Tangente wissen wir bereits, dass \$f(3)=9\$ und \$f'(3)=6\$.
Setzen wir dies in die Normalengleichung ein, so erhält man als Gleichung für die Normale den Term
\$n(x)=- 1/6 *(x-3)+9=- 1/6 x +3/6 +9=- 1/6 x+9,5\$.