1. Motivation
Erkenntnisse über die Symmetrieeigenschaften eines Graphen können nützlich sein, um diesen zu zeichnen.
In unserem Fall behandeln wir nur die Achsensymmetrie zur y-Achse und die Punktsymmetrie zum Ursprung. Auch Symmetrien zu anderen Achsen und Punkten wären jedoch denkbar.
2. Achsensymmetrie zur y-Achse
2.1. Definition
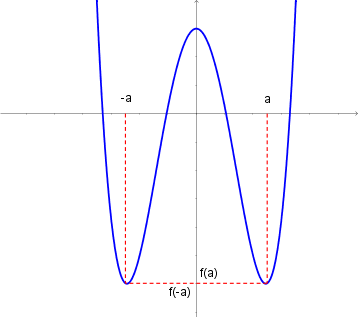
Weist der Graph einer Funktion eine Achsensymmetrie zur y-Achse auf, so befindet sich neben einem Punkt \$P(a|f(a))\$ auch der an der y-Achse gespiegelte Punkt \$P'(-a|f(a))\$ auf dem Graph. Dies gilt für alle Werte von \$a\$.
Aus dem Schaubild kann man entnehmen, dass im Falle der Achsensymmetrie stets \$f(-a)=f(a)\$ ist.
Somit gilt:
Achsensymmetrie zur y-Achse
Wenn man nachweisen kann, dass \$f(-a)=f(a)\$ für alle \$a in D\$, dann ist der \$G_f\$, also der Graph von f, achsensymmetrisch zur y-Achse.
2.2. Beispiele zum Nachweis der Achsensymmetrie
Überprüfe die folgenden Beispiele auf Achsensymmetrie zur y-Achse:
-
\$f(x)=x^4-x^2+1\$
-
\$g(x)=e^x+e^{-x}\$
Lösung:
-
\$f(-x)=(-x)^4-(-x)^2+1=x^4-x^2+1=f(x)\$
Da \$f(-x)=f(x)\$ gilt, unabhängig vom Wert von x, ist der Graph der Funktion f achsensymmetrisch zur y-Achse.
-
\$g(-x)=e^{-x}+e^{-(-x)}=e^{-x}+e^x=g(x)\$
Auch hier gilt wieder, dass \$g(-x)=g(x)\$ ist, so dass auch \$G_g\$ achsensymmetrisch zur y-Achse ist.
3. Punktsymmetrie zum Ursprung
3.1. Definition
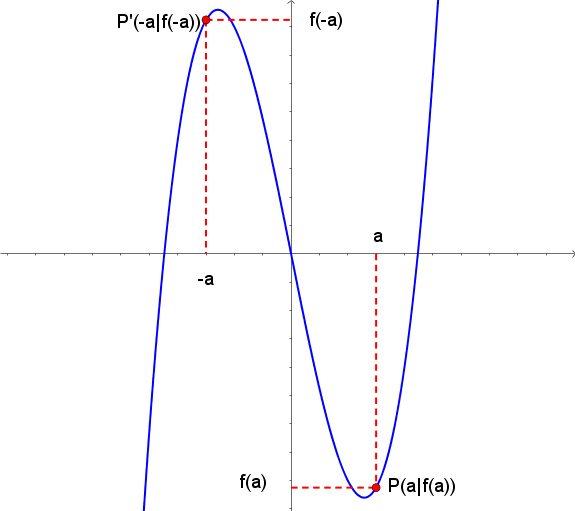
Analog wir bei der Achsensymmetrie zur y-Achse muss für jeden Punkt \$P(a|f(a))\$ gelten, dass auch sein Spiegelpunkt \$P'(-a|f(-a))\$ auf dem Graph liegt, wobei nun gelten muss, dass \$f(-a)=-f(a)\$ ist für alle a aus dme Definitionsbereich.
Punktsymmetrie zum Ursprung
Wenn für alle \$a in D\$ gilt, dass \$f(-a)=-f(a)\$ ist, so ist \$G_f\$ punktsymmetrisch zum Ursprung.
3.2. Beispiele zum Nachweis der Punktsymmetrie
Überprüfe die folgenden Beispiele auf Punktsymmetrie zum Ursprung:
-
\$f(x)=-x^3+x\$
-
\$g(x)=x^2 / {x^3-x}\$
Lösungen:
-
\$f(-x)=-(-x)^3+(-x)=-(-x^3)-x=x^3-x=\$
\$=-(-x^3+x)=-f(x)\$
Somit ist die Bedingung \$f(-x)=-f(x)\$ für die Punktsymmetrie im Ursprung erfüllt.
-
\$g(-x)=(-x)^2 /{(-x)^3-(-x)}=x^2 / {-x^3+x}=\$
\$=x^2/ {-(x^3-x)}=- {x^2}/{x^3-x}=-g(x)\$
Somit ist auch der Graph dieser Funktion punktsymmetrisch zum Ursprung.
4. Ganzrationale Funktionen und Symmetrie
Funktionen der Form \$a_n*x^n+a_{n-1}*x^{n-1}+...+a_1*x^1+a_0\$ mit \$a_n!=0, a_i in RR (iin {0,1,2, ...,n}), n in NN\$ heißen ganzrationale Funktionen vom Grad n. Der Grad entspricht hierbei der höchsten vorkommenden Potenz.
Beispiele:
-
\$f(x)=x^3+2x-1\$ ist eine ganzrationale Funktion vom Grad 3.
-
\$g(x)=-2x^2+4x^7\$ ist eine ganzrationale Funktion vom Grad 7.
-
\$2x^0=2\$ ist eine ganzrationale Funktion vom Grad 0.
Mit den Definitionen der vorangegangenen Artikeln wird deutlich:
Symmetrie bei ganzrationalen Funktionen
Eine ganzrationale Funktion, in der nur ungerade Potenzen vorkommen, ist punktsymmetrisch zum Ursprung, eine mit ausschließlich geraden Potenzen hingegen achsensymmetrisch zur y-Achse.
Beispiele:
-
\$f(x)=x^7+x^5-2x\$ enthält nur ungerade Hochzahlen (\$2x=2x^1\$), wodurch \$G_f\$ punktsymmetrisch zum Ursprung ist.
-
\$g(x)=x^4-2\$ enthält nur gerade Hochzahlen (\$-2=-2x^0\$, wobei die Null zu den geraden Zahlen gehört), wodurch \$G_g\$ achsensymmetrisch zur y-Achse ist.
-
\$h(x)=x^3-x^2\$ enthält gerade und ungerade Hochzahlen, so dass \$G_h\$ weder achsensymmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung ist.
5. Sinus und Kosinus
Symmetrie des Sinus und Kosinus:
Es gilt:
\$cos(-x)=cos(x)\$ (punktsymmetrisch zum Ursprung)
und
\$sin(-x)=-sin(x)\$ (achsensymmetrisch zur y-Achse).