1. Motivation
Beispielaufgabe aus Klasse 7
Petra möchte ein Bad nehmen und lässt in die zu Beginn leere Badewanne 5 Minuten lang Wasser mit der Fließgeschwindigkeit \$z(t)=20\$ ein, wobei die Fließgeschwindigkeit in \$l/min\$ angegeben wird.
Als sie nach dem Bad den Stöpsel zieht, fließt das Wasser mit konstanter Fließgeschwindigkeit wieder ab, so dass die Badewanne nach 10 Minuten geleert ist.
-
Zeichne das Schaubild des aktuellen Wasserstands in der Badewanne beim Einlassen des Wasssers und in das gleiche Koordinatensystem das Schaubild der zugehörigen Fließgeschwindigkeit zu jedem Zeitpunkt. Bestimme für beide Schaubilder die zugehörigen Funktionsterme Z(t) für den Wasserstand zum Zeitpunkt t und z(t) für die Fließgeschwindigkeit zum Zeitpunkt t.
-
Wiederhole diese Schritte für den Fall des Abfließens des Wassers. Gib entsprechend die Funktionsterme A(t) und a(t) an.
Lösung:
Teilaufgabe 1:
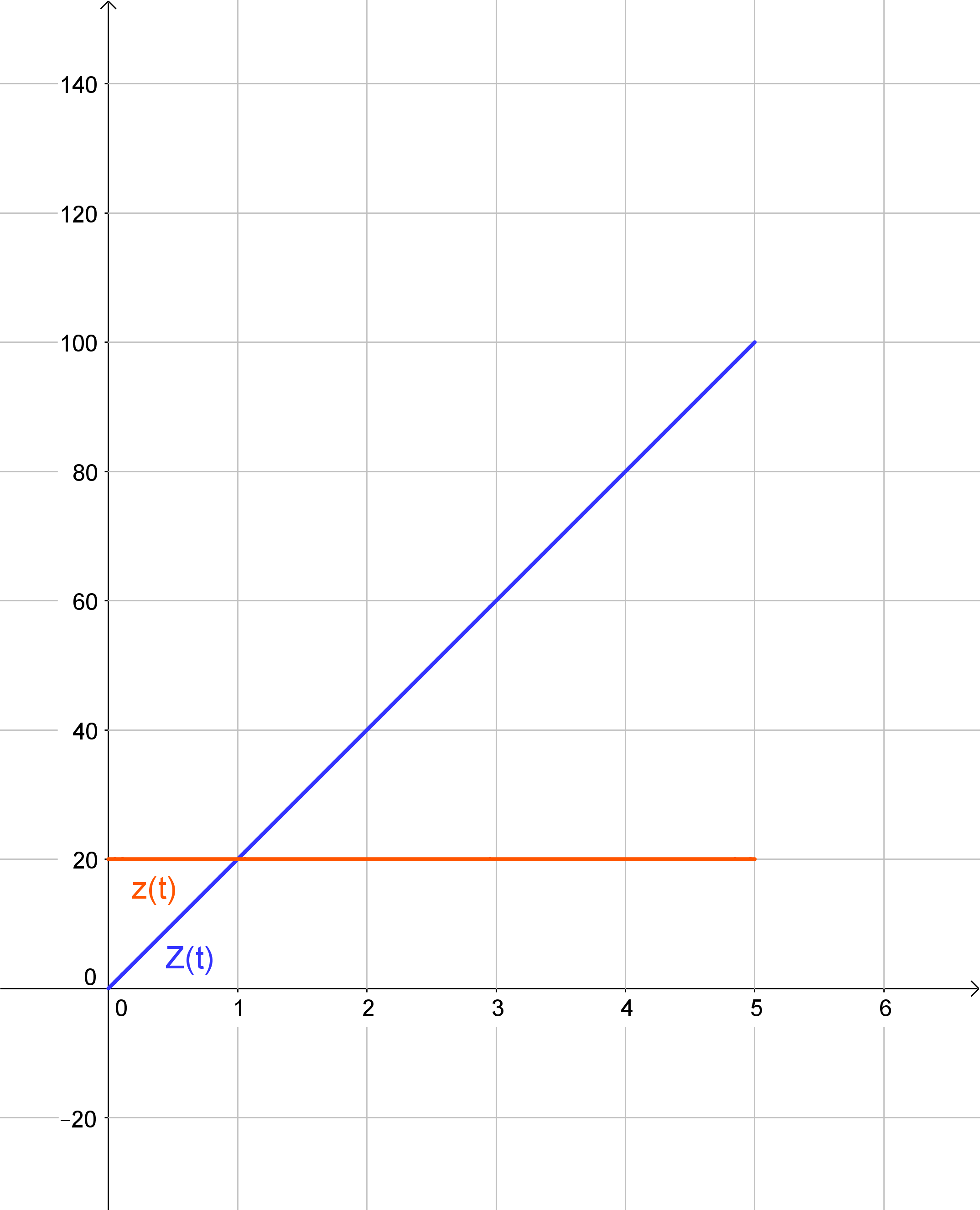
Der Term für die Fließgeschwindigkeit lautet \$z(t)=20\$, der für den Wasserstand zum Zeitpunkt t \$Z(t)=20*t\$.
Teilaufgabe 2:
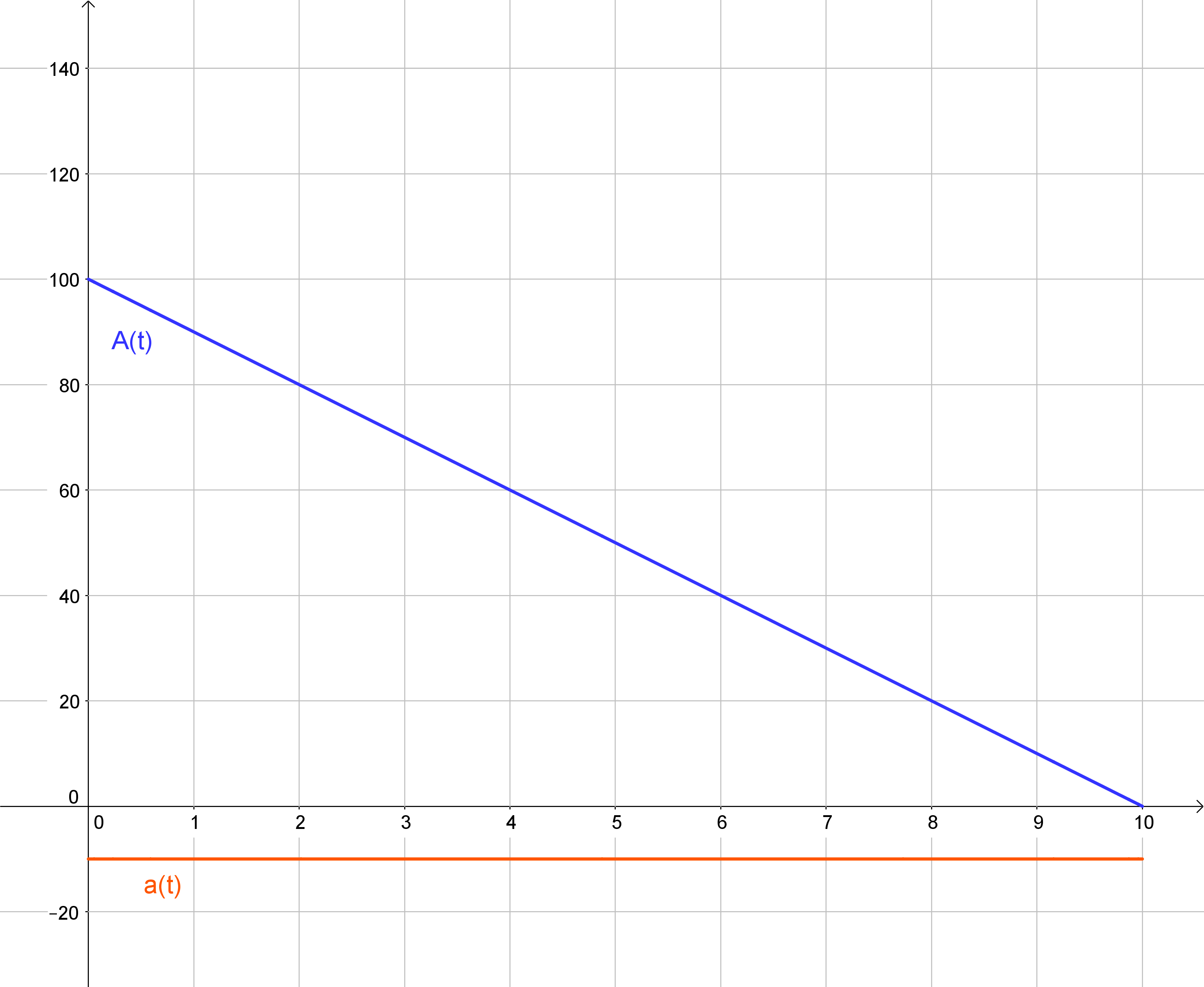
Zu Beginn des Abfließens sind 100 Liter in der Badewanne, wobei sich diese in 10 Minuten vollständig entleert, so dass 10 \$l/min\$ abfließen. Das entspricht bereits dem Funktionsterm von \$a(t)=-10\$. Das negative Vorzeichen kommt dadurch zustande, dass das Abfließen von Wasser einem negativen Zufluss entspricht.
Für den Funktionsterm des aktuellen Wasserstands gilt in diesem Fall \$A(t)=100-10*t\$, da zu Beginn 100 Liter in der Badewanne sind und pro Minute 10 Liter abfließen.
2. Zusammenhang zwischen z(t) und Z(t)
2.1. Graphischer Zusammenhang
Die Aufgaben aus dem letzten Abschnitt führen zu der Frage, inwieweit diese Aufgaben einem neuen Themengebiet, namentlich der Integralrechnung zuzuordnen sind, da sie beide komplett mit bisherigen Mitteln zu lösen sind.
Um diese Frage zu klären, soll nun der Zusammenhang zwischen z(t) und Z(t) genauer betrachtet werden: Z(t) liefert für einen eingesetzten Wert t den Wasserstand in Litern zu diesem Zeitpunkt zurück. So ist beispielsweise \$Z(2)=40\$, was nichts anderes bedeutet, als dass 2 Minuten nach Beginn des Einfließens des Wassers 40 Liter in der Badewanne sind.
Diesen Wert kann man auch über \$z(t)=20\$ erhalten, denn z(t) liefert zu jedem Zeitpunkt die momentane Zuflussgeschwindigkeit in Litern pro Minute zurück. In unserem einfachen Fall sind das immer \$20 l/min\$. Nach zwei Minuten sind also \$2*20 min * l/min=40 l\$ in die Badewanne geflossen. Da diese anfangs leer war, entsprechen diese 40 Liter dem Wasserstand in der Badewanne zum Zeitpunkt 2 Minuten.
Wir haben also die momentane Zuflussgeschwindigkeit mit der Dauer des Zuflusses multipliziert, was man graphisch als Rechtecksfläche interpretieren kann:

Und diese Rechtecksfläche entspricht dem Funktionswert von Z(2). Man kann Z(t) also als Maß für den Flächeninhalt interpretieren, der vom Schaubild von z(t) und der t-Achse im Intervall von 0 bis t eingeschlossen wird. Somit entspricht jeder Funktionswert Z(t) dem Flächeninhalt unter z(t) zwischen 0 und t.
Um den Flächeninhalt der Fläche zwischen dem Graphen einer Funktion f(x) und der x-Achse auf dem Intervall [a ; b] zu beschreiben, gibt es eine spezielle Schreibweise, nämlich
\$int_a^b f(x) dx\$
a und b sind hier die untere und die obere Integrationsgrenze, f(x) heißt in diesem Zusammenhang Integrand und der gesamte Ausdruck wird gesprochen als "Integral von a bis b über f(x) dx". Das "dx" legt fest, über welche Variable integriert wird, hier ist die Integrationsvariable somit x.
Auf unser Beispiel angewendet würde das für die Fläche \$A_1\$ bedeuten:
\$A_1=int_0^2 z(t) dt\$.
Das steht also für die Fläche zwischen dem Graph von z(t) und der t-Achse (daher auch dt und nicht dx) auf dem Intervall von 0 bis 2 und entspricht somit der schraffierten Fläche \$A_1\$ im Schaubild.
Weitere Beispiele wären:
-
\$int_1^3 z(t) dt = 40\$
-
\$int_2^2 z(t) dt = 0\$ (das eingeschlossene Rechteck hat die Breite 0)
-
\$int_3^1 z(t) dt=-40\$ (hier wird von rechts nach links integriert, so dass ein negativer Flächeninhalt herauskommt)
Wie man am letzten Beispiel sieht, liefert das Integral nicht den geometrischen Flächeninhalt der eingeschlossenen Fläche zurück, der immer positiv wäre, sondern den sogenannten orientierten Flächeninhalt, der auch negative Werte annehmen kann.
Das Beispiel \$int_1^3 z(t) dt\$ entspricht der Wassermenge, die zwischen der ersten und der dritten Minute hinzugekommen ist. Eine alternative Möglichkeit der Berechnung wäre, von der Wassermenge zum Zeitpunkt t=3 die Wassermenge zum Zeitpunkt t=1 abzuziehen, also \$int_1^3 z(t) dt=Z(3)-Z(1)\$ zu berechnen. Für unser Beispiel lässt sich also verallgemeinern:
\$int_a^b z(t) dt = Z(b) - Z(a)\$
Überprüfen wir unsere Erkenntnisse an einem zweiten Beispiel, nämlich an den Graphen der Funktionen a(t) und A(t):
\$int_2^4 a(t) dt = A(4) - A(2) = 60 - 80 = -20\$
Alternativ hätten wir auch den orientierten Flächeninhalt auf dem Intervall von 2 bis 4 zwischen dem Graph von a(t) und der t-Achse berechnen können, was \$int_2^4 a(t) dt = -10 * (4-2)= -20\$ liefert. Beachte, dass auch hier wieder ein negativer Flächeninhalt auftritt. Zwar wurde diesmal von links nach rechts integriert, allerdings für Werte unter der t-Achse, so dass auch hier ein negativer Zahlenwert sinnvoll ist.
2.2. Zusammenhang über die Ableitung
Ein weiterer Zusammenhang, der vielleicht schon aufgefallen ist, ist die Tatsache, dass z(t)=Z´(t) ist, denn
\$Z(t)=20*t\$
\$Z´(t)=20=z(t)\$
Dies gilt auch für den Zusammenhang zwischen a(t) und A(t), denn
\$A(t)=100-10*t\$
\$A´(t)=-10=a(t)\$
Ist dies ein seltsamer Zufall oder lässt sich dieser Zusammenhang über die Ableitung verallgemeinern?
2.3. Hauptsatz der Differenzial- und Integralrechnung
Um die Vermutung aus dem letzten Abschnitt zu beweisen, führen wir zunächst eine spezielle Funktion ein, nämlich die Integralfunktion \$I_a(t)=int_a^t f(x) dx\$. Sie liefert den Flächeninhalt zwischen der Funktion f(x) und der x-Achse zurück, wobei die linke Integrationsgrenze festgelegt ist (hier a) und die rechte jeden beliebigen Wert annehmen kann. Ein Beispiel für diese Integralfunktion hatten wir schon in der Einführungsaufgabe:
\$int_0^t z(t) dt=Z(t)-Z(0)=Z(t)\$
Das bedeutet, dass Z(t) dem Flächeninhalt zwischen der festen unteren Grenze 0 und der variablen oberen Grenze t entspricht. So gilt z. B.
-
\$Z(2)=int_0^2 z(t) dt\$
-
\$Z(3)=int_0^3 z(t) dt\$
-
usw.
Somit entspricht \$Z(t)\$ der Integralfunktion \$I_0(t)=int_0^t z(t) dt\$.
Nun wollen wir für unseren speziellen Fall zeigen, dass gilt: \$Z´(t)=z(t)\$ mit \$Z(t)=I_0(t)=int_0^t z(t) dt\$. Wir müssten also zeigen, dass die Ableitung von \$int_0^t z(t) dt\$ die Funktion \$z(t)\$ selbst ergibt.
Genau das zeigt der
Hauptsatz der Differenzial- und Integralrechnung:
Bildet man die Ableitungsfunktion der Integralfunktion \$I_a(x)=int_a^x f(t) dt\$, so erhält man die Integrandenfunktion f, kurz: \$I_a´(x)=f(x)\$.
Dabei muss f stetig sein, wodurch \$I_a\$ differenzierbar ist.
|
Beachte, dass hier \$I_a(x)=int_a^x f(t) dt\$ statt \$I_a(x)=int_a^x f(x) dx\$ verwendet wird. Beide Ausdrücke sind formal identisch, allerdings erleichtert die Einführung des t als Integrationsvariable die Unterscheidung zwischen der Integrationsvariable t und der oberen variablen Grenze x. |
Beweis:
Leiten wir \$I_a(x)\$ ab:
\$I_a´(x)=lim_{h->0} {I_a(x+h)-I_a(x)}/h\$
Setzt man die Definition \$I_a(x)=int_a^x f(t) dt\$ der Integralfunktion ein, so erhält man
\$lim_{h->0} {int_a^{x+h} f(t) dt-int_a^x f(t) dt}/h\$
Der Zähler lässt sich als \$int_a^{x+h} f(t) dt-int_a^x f(t) dt=int_x^{x+h}f(t)dt\$ schreiben, wie man aus der Grafik ablesen kann, denn von der gesamten Fläche \$int_a^{x+h} f(t) dt\$ (alles, was blau schraffiert ist) wird die rot schraffierte Fläche \$int_a^x f(t) dt\$ abgezogen, wodurch die ausschließlich blau schraffierte Fläche übrigbleibt, die durch das Integral \$int_x^{x+h}f(t)dt\$ beschrieben wird:
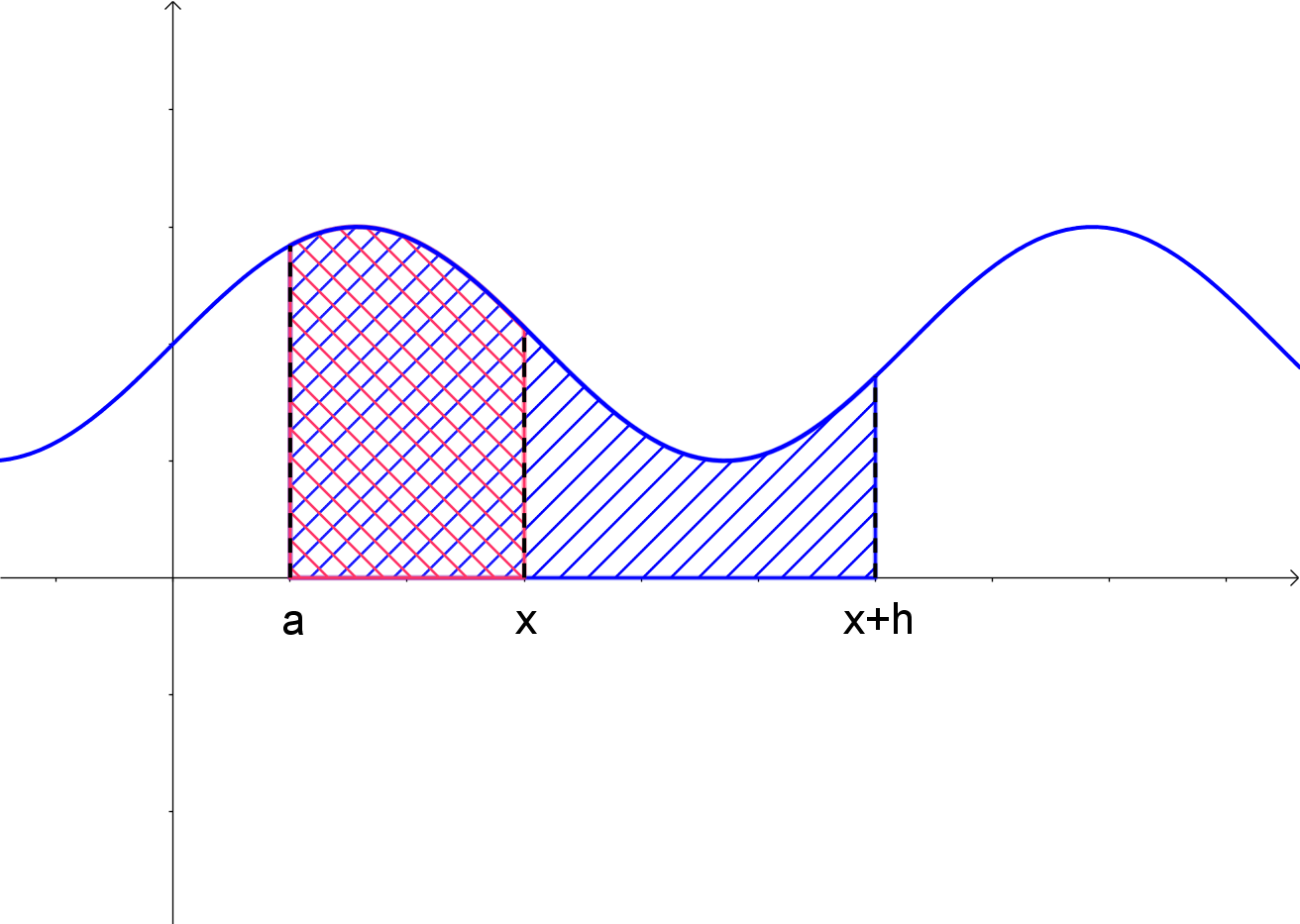
Somit erhalten wir für die Ableitung der Integralfunktion den Ausdruck
\$I_a´(x)= lim_{h->0} {int_x^{x+h}f(t)dt}/h\$
Leider können wir mit dem x+h als obere Grenze nicht weiterkommen und bedienen uns des folgenden Tricks:
Da f nach Voraussetzung stetig ist (in unserem Fall bedeutet das "durchgängig zeichenbar"), so existiert ein Wert \$z in [x ; x+h\$] mit \$f(z)*h=int_x^{x+h} f(t)dt\$.
Das bedeutet, dass es ein Rechteck der Breite h und der Höhe f(z) gibt (mit z zwischen x und x+h), so dass der Flächeninhalt dieses Rechtecks dem Wert des Integrals entspricht.
Graphisch kann man an unserem Beispiel zeigen, dass es einen Wert k auf [x ; x+h] gibt, so dass der Flächeninhalt des Rechtecks der Breite h und der Höhe f(k) auf jeden Fall kleiner oder gleich dem gesuchten Flächeninhalt \$int_x^{x+h}f(t)dt\$ ist. Zum Beispiel wählt man dazu die Stelle k auf der x-Achse, an der der Funktionswert von f minimal wird.
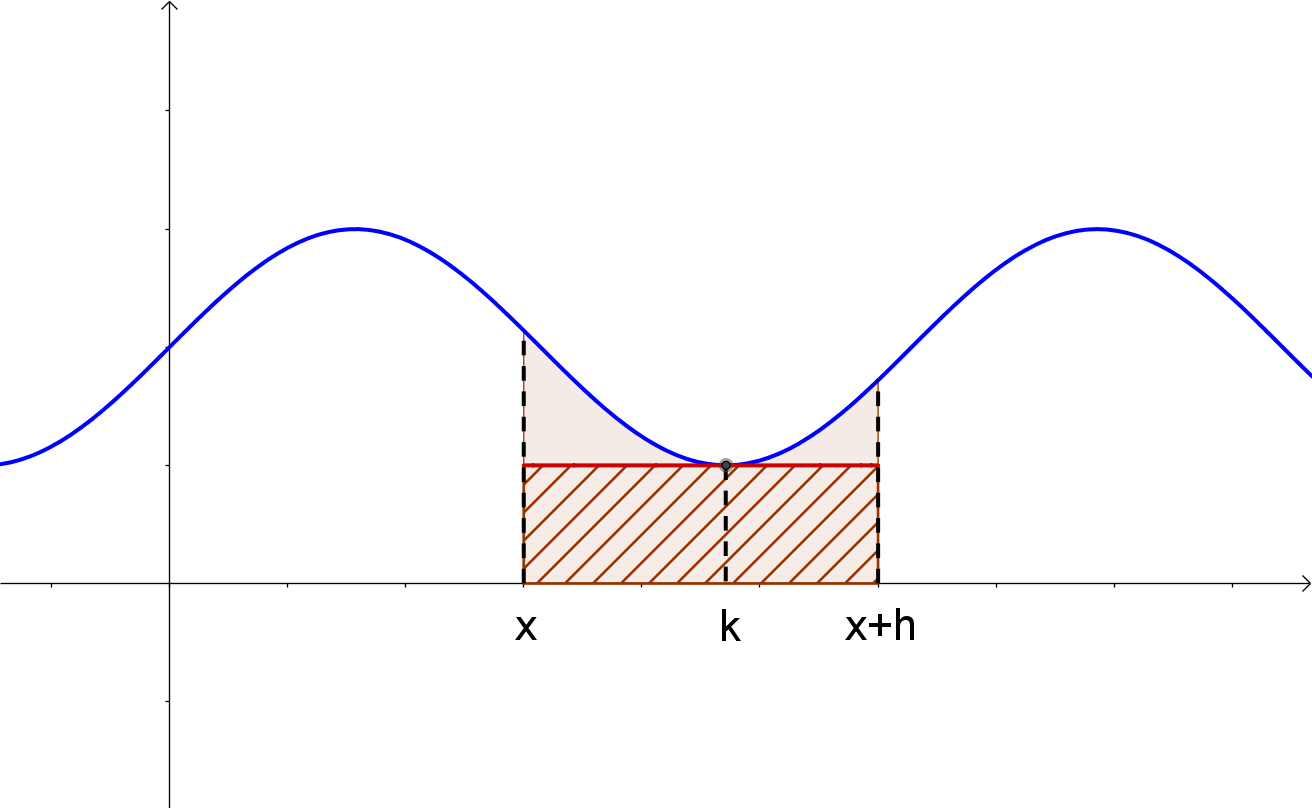
Ebenso ist in diesem Beispiel der Flächeninhalt des Rechtecks, das in diesem graphischen Beispiel die Höhe f(x) hat, größer gleich dem Wert des Integrals:
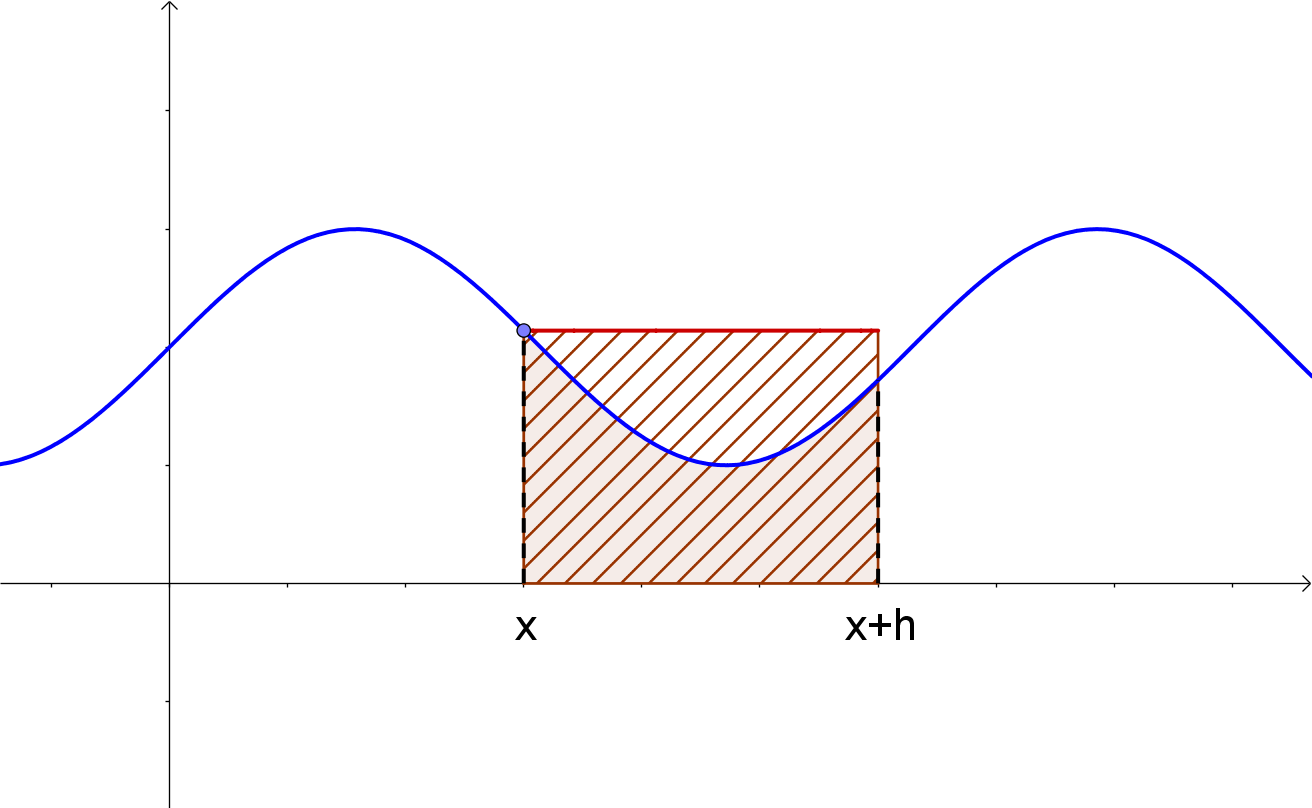
Da f stetig ist, werden auch alle Zwischenwerte zwischen f(k) und f(x) angenommen, so dass es einen Wert z gibt, der auf jeden Fall zwischen x und x+h liegt und für den der Flächeninhalt des Rechtecks der Breite h und der Höhe f(z) genau dem Wert des Integrals entspricht:
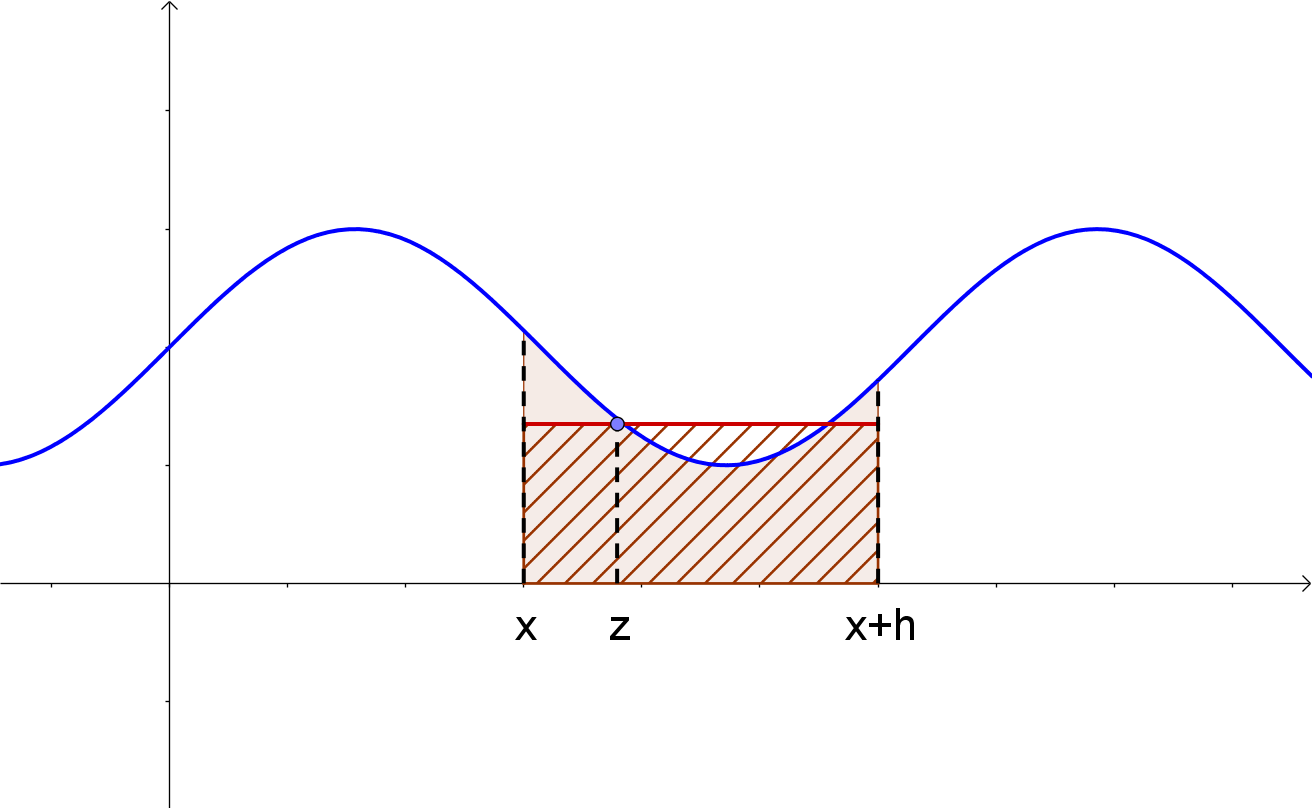
Insgesamt verhilft uns diese Erkenntnis dazu, den Term \$I_a´(x)= lim_{h->0} {int_x^{x+h}f(t)dt}/h\$ wegen \$f(z)*h=int_x^{x+h} f(t)dt\$ umzuschreiben zu
\$I_a´(x)= lim_{h->0} {f(z)*h}/h=lim_{h->0}f(z)\$
Da wir wissen, dass \$x <= z <= x+h\$ ist, d. h. mit \$h->0\$ läuft auch \$z->x\$. Da f eine stetige Funktion ist, gilt dadurch auch, dass \$lim_{h->0} f(z)=lim_{z->x}f(z)=f(x)\$ ist.
Damit haben wir gezeigt, dass \$I_a´(x)=f(x)\$ ist, was zu beweisen war.
Bezogen auf unser Beispiel mit dem Zufluss des Wassers in die Badewanne bedeutet das, dass \$Z´(t)=z(t)\$ ist, was wir schon zu Beginn vermutet hatten.
3. Die Stammfunktion
Stammfunktion
Eine Funktion F(x) heißt Stammfunktion von f(x), wenn gilt, dass F´(x)=f(x).
Bezogen auf unser Badewannenbeispiel ist die Funktion Z(t) (also die Funktion, die zu jedem Zeitpunkt den Wasserstand zurückgibt) die Stammfunktion von z(t) (die Funktion, die zu jedem Zeitpunkt die momentane Änderungsrate zurückliefert).
Denn \$Z(t)=20*t\$ und \$Z´(t)=20=z(t)\$, was nach Definition bedeutet, das Z(t) die Stammfunktion von z(t) ist.
Um eine Stammfunktion F(x) einer Funktion f(x) zu erhalten muss man f(x) "rückwärts ableiten". Ein Beispiel soll das veranschaulichen:
\$f(x)=cos(x)\$
Nun sucht man als Stammfunktion eine Funktion, die abgeleitet \$cos(x)\$ ergibt, also beispielsweise \$sin(x)\$. Weitere Beispiele für Stammfunktionen von \$cos(x)\$ wären \$sin(x)+1\$ oder \$sin(x)-2\$, da diese nur parallel verschoben sind und somit an jeder Stelle die gleich Steigung aufweisen wie \$sin(x)\$.
Somit lässt sich die Menge aller Stammfunktionen von \$f(x)=cos(x)\$ notieren als
\$F(x)=sin(x)+c text( mit ) c in RR\$
4. Berechnung des orientierten Flächeninhalts mit Hilfe des Integrals
In einem der vorigen Abschnitte hatten wir bereits gezeigt, dass man das zwischen zwei Zeitpunkten a und b in die Badewanne gelaufene Wasser auf zwei Arten berechnen kann:
-
Die Fläche zwischen dem Graphen von z(t) und der Zeitachse auf dem Intervall [a;b] berechnen
-
Den Wasserstand in der Wanne zum Zeitpunkt a vom Wasserstand zum Zeitpunkt b abziehen, also Z(b)-Z(a)
Zusammengefasst also
\$int_a^b z(t) dt = Z(b) - Z(a)\$
Da beide Berechnungen zum selben Ergebnis führen, könnte man für die Flächenberechnung auch die Methode mit den Differenzen verwenden.
Beispiel:
Aufgabe:
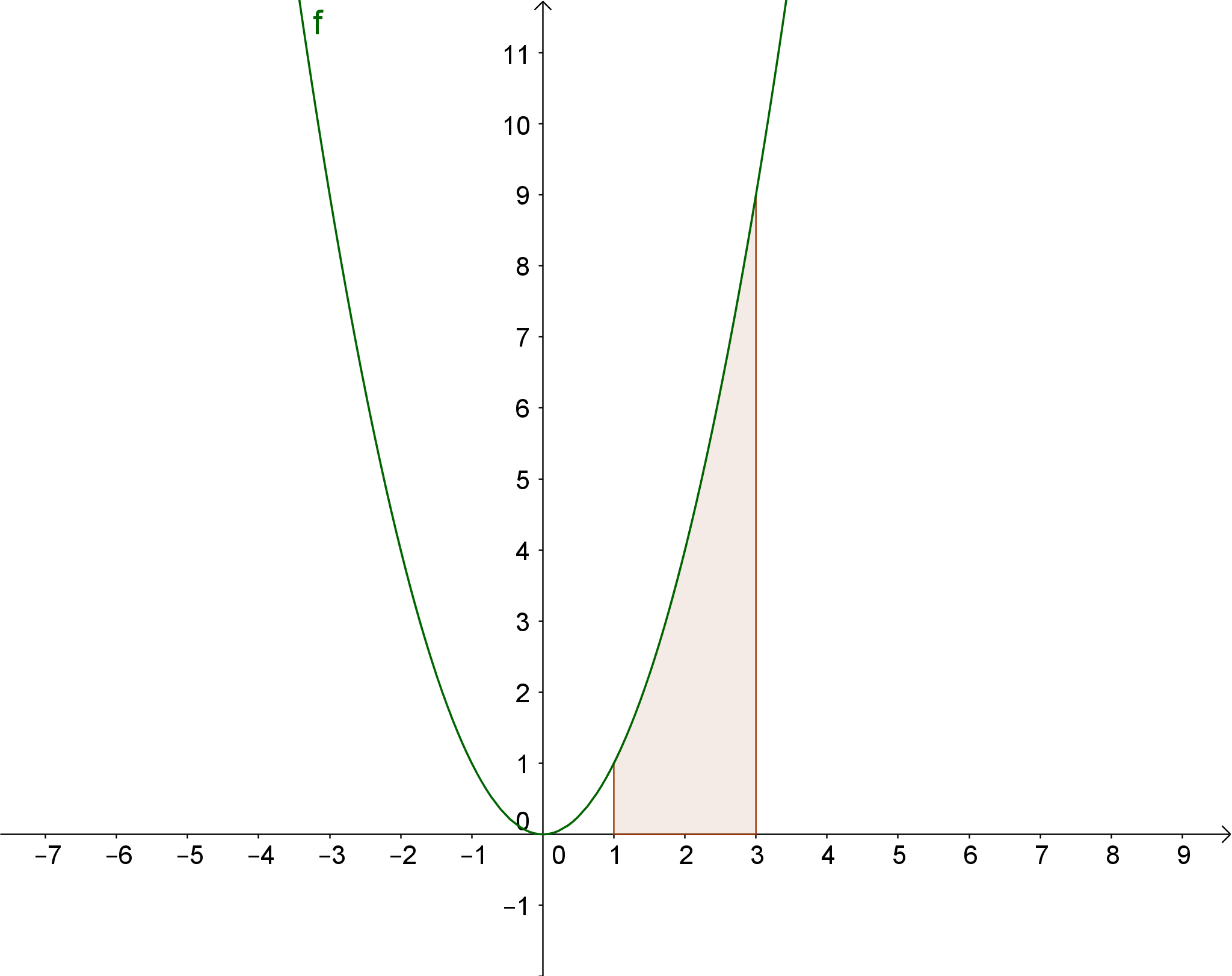
Berechne \$int_1^3 x^2 dx\$.
Lösung:
Wenn wir eine Stammfunktion F(x) von \$x^2\$ kennen, müssten wir F(3) - F(1) berechnen, um den Flächeninhalt zu erhalten.
Eine mögliche Stammfunktion von \$f(x)=x^2\$ wäre z. B. \$F(x)=1/3 * x^3\$, denn \$F´(x)=3* 1/3 *x^2=x^2=f(x)\$.
Berechnet man nun \$F(3)-F(1)\$ so erhält man \$1/3 * 3^3 - 1/3 * 1^3=9-1/3=26/3\$.
Nun gibt es nur noch eine offene Frage: was wäre passiert, wenn man in der Berechnung statt \$F(x)=1/3 * x^3\$ eine andere mögliche Stammfunktion, wie z. B. \$1/3 * x^3 -1\$ verwendet hätte?
Überprüfen wir das allgemein:
Dazu führen wir eine weitere Stammfunktion \$G(x)=F(x)+c text( mit )c in RR\$ ein und berechnen das Ergebnis von \$int_a^b f(x) dx = F(b)-F(a)\$ mit der Stammfunktion \$G(x)\$:
\$G(b)-G(a)=F(b) + c - (F(a) +c)=F(b) + c - F(a) -c= F(b) - F(a)\$
Dieses Ergebnis zeigt, dass es egal ist, welche Stammfunktion man für die Berechnung heranzieht.
Mit korrekter Notation gilt somit allgemein:
\$ int_a^b f(x) dx = [F(x)]_a^b = F(b)-F(a) \$
wobei F(x) eine beliebige Stammfunktion von f(x) ist.
Angewendet auf unser Beispiel bedeutet das:
\$ int_1^3 x^2 dx = [ 1/3 * x^3 ]_1^3 = 1/3 * 3^3 - 1/3 *1^3 =26/3 \$
Graphisch betrachtet haben wir somit den Flächeninhalt zwischen dem Schaubild von \$f(x)=x^2\$ und der x-Achse auf dem Intervall von 1 bis 3 berechnet, was hier nochmals graphisch gezeigt ist.