1. Motivation
Aufgabe:
Die von \$x^3\$ Bakterien in einer Petrischale bedeckte Fläche soll durch die Funktion \$f(x)=e^x\$ beschrieben werden (\$x\$ in Stunden, \$f(x)\$ in \$cm^2\$).
-
Berechne, welche Fläche nach 2 Stunden bedeckt ist.
-
Gib an, wann genau 5 \$cm^2\$ von den Bakterien bedeckt sind.
Lösung:
Um zu berechnen, welche Fläche nach 2 Stunden bedeckt ist, muss \$f(2)=e^2~~7,39\$ \$cm^2\$ berechnet werden.
Der umgekehrte Fall ist etwas kniffliger, denn zu lösen ist nun die Gleichung \$f(x)=5\$, also \$e^x=5\$.
Zeichnet man die Situation in ein Schaubild, so kann man die Aufgabe graphisch lösen:
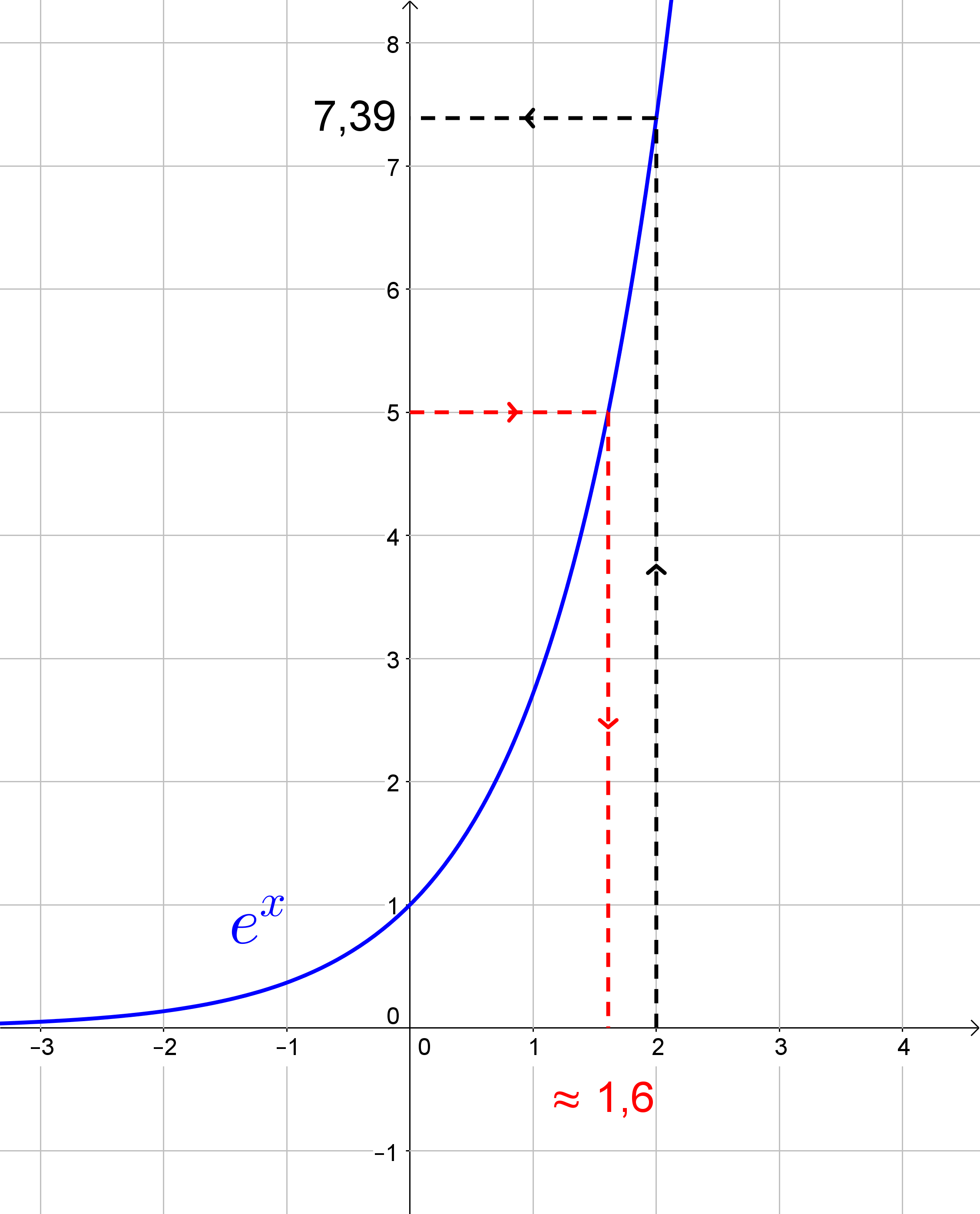
Schwarz gestrichelt kann man den ersten Teil der Aufgabe erkennen: man startet bei der 2 auf der x-Achse und erhält über den Graphen von f den y-Wert 7,39, wie oben berechnet.
Rot gestrichelt sieht man die Lösung zum zweiten Teil: nun starten wir bei 5 auf der y-Achse und erhalten als x-Wert in etwas 1,6. Die Probe ergibt \$e^{1,6}~~4,953\$. Wir sind also schon ziemlich nah dran, aber perfekt ist es noch nicht.
2. Der natürliche Logarithmus
2.1. Definition
Der natürliche Logarithmus
Man nennt die Zahl, mit der man \$e\$ potenzieren muss, um a zu erhalten, den natürlichen Logarithmus von a, kurz \$ln(a)\$ (kleines L und kleines N für "logarithmus naturalis").
Diese Zahl ist auch die Lösung der Gleichung \$e^x=a\$ mit \$a>0\$, also \$e^{ln(a)}=a\$.
Eine alternative Bezeichnungsweise für den natürlichen Logarithmus ist der Logarithmus zur Basis \$e\$, was auch als \$log_e(a)\$ bezeichnet werden könnte (sprich: "Logarithmus von a zur Basis e").
2.2. Logarithmus-Gesetze mit Beispielen
Der Logarithmus ist bereits von früher bekannt und von daher auch die Logarithmus-Gesetze, die unverändert auch für den natürlichen Logarithmus gelten:
Logarithmus-Gesetze:
-
\$ln(a*b)=ln(a)+ln(b)\$
-
\$ln(a/b)=ln(a)-ln(b)\$
-
\$ln(a^b)=b*ln(a)\$ ("Hut-ab-Regel")
Dazu einige Beispiele:
-
\$ln(x*e)=ln(x)+ln(e)=ln(x)+1\$
-
\$ln(1/e)=ln(1)-ln(e)=0-1=-1\$
-
\$ln(e^2)=2*ln(e)=2*1=2\$
2.3. Lösung der Eingangsaufgabe
Mit Hilfe des natürlichen Logarithmus und seiner Gesetze können wir die Aufgabe von oben nun exakt lösen:
\$e^x=5 | ln\$
\$ln(e^x)=ln(5)\$
Mit dem 3. Logarithmus-Gesetz erhält man
\$x*ln(e)=ln(5)\$
Nach der Definition des natürlichen Logarithmus ist \$ln(e)\$ die Zahl, mit der man \$e\$ potenzieren muss um \$e\$ zu erhalten. Das ist hier natürlich die 1, d. h. \$ln(e)=1\$. Somit wird unsere Gleichung zu
\$x*1=x=ln(5)~~1,609\$
2.4. Spezielle Werte des ln
Ein weiterer spezieller Wert des Logarithmus ist übrigens \$ln(1)\$, nämlich die Zahl, mit der man \$e\$ potenzieren muss, um 1 zu erhalten. Das ist die 0, denn \$e^0=1\$. Somit gilt auch \$ln(1)=0\$.
Einige besondere Werte des natürlichen Logarithmus:
-
\$ln(e)=1\$
-
\$ln(1)=0\$
-
\$ln(e^2)=2*ln(e)=2*1=2\$
-
\$ln(e^3)=3\$
Für Werte kleiner gleich 0 ist der Logarithmus nicht definiert, da es auch keine Zahl gibt mit der man \$e\$ potenzieren kann, um etwas Negatives zu erhalten. Schließlich nimmt die e-Funktion auf dem gesamten Definitionsbereich \$RR\$ positive Werte an.
2.5. Exponentialgleichungen mit anderer Basis als e
Aufgabe:
Bestimme ein \$x\$ so, dass \$2^x=10\$ ist.
Eine direkte Lösung dafür wäre \$x=log_2 (10)\$, also der Logarithmus von 10 zur Basis 2. Leider gibt es nicht auf allen Taschenrechnern dafür eine entsprechende Taste.
Probieren wir es mit dem natürlichen Logarithmus:
\$2^x=10 | ln\$
\$ln(2^x)=ln(10)\$
\$x*ln(2)=ln(10) | : ln(2)\$
\$x={ln(10)}/{ln(2)}~~3,322\$
Probe: \$2^{3,322}~~10,000\$, stimmt also.
Wenn man die 2 mit a und die 10 mit b ersetzt ergibt sich die Gleichung \$a^x=b\$ mit der Lösung \$x={ln(b)}/{ln(a)}\$. Zusammengefasst:
Allgemeine Exponentialgleichung:
Die Gleichung
\$a^x=b\$
mit \$a, b>0\$ hat die Lösung
\$x={ln(b)}/{ln(a)}\$.
2.6. Graph der natürlichen Logarithmusfunktion
Der Graph der natürlichen Logarithmusfunktion sieht so aus:
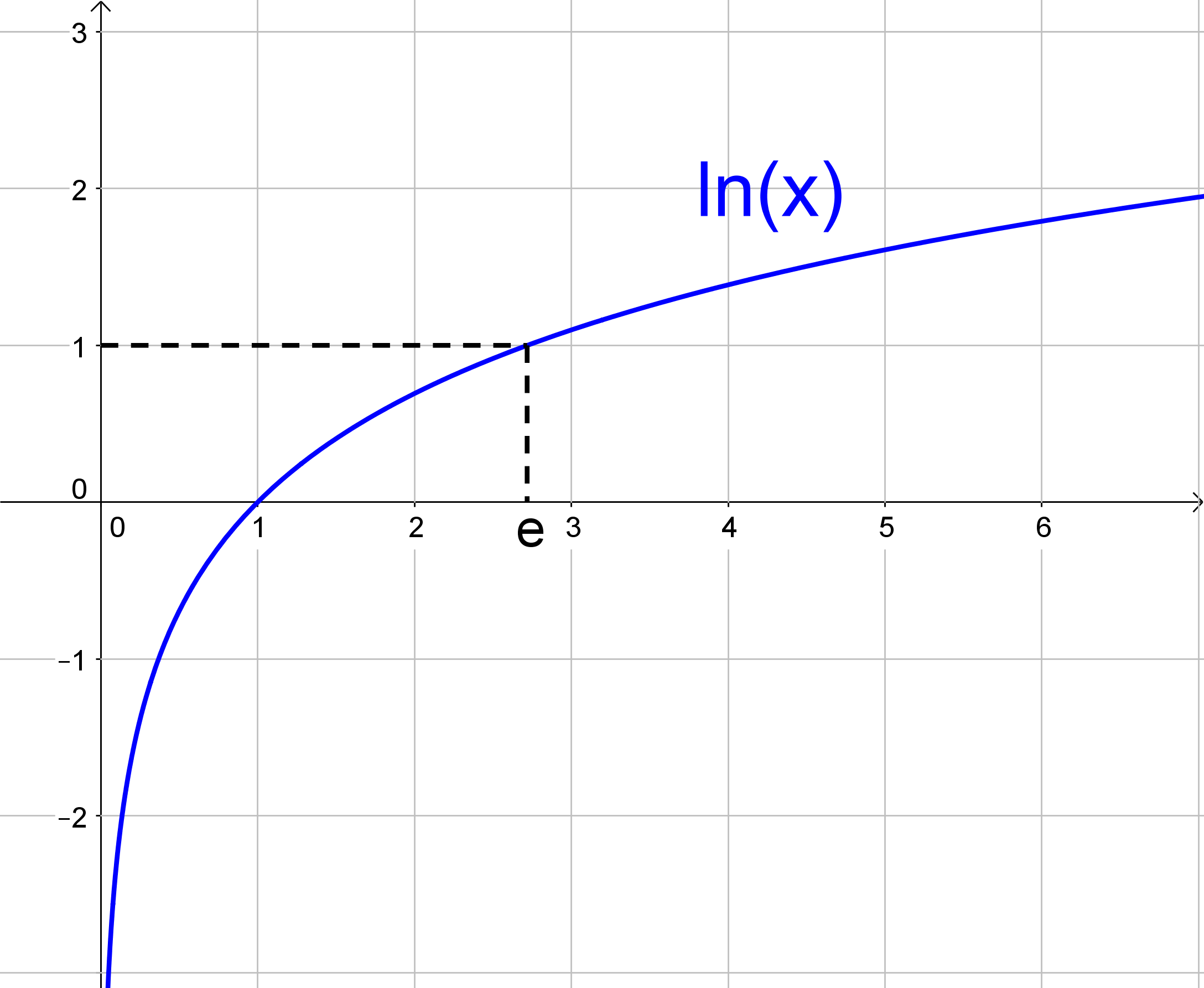
Man sieht hier nochmal die besonderen Werte des natürlichen Logarithmus: \$ln(1)=0\$ und \$ln(e)=1\$.
Wie oben bereits erwähnt, ist er nur für positive x-Werte definiert und strebt für \$x->0\$ gegen \$-oo\$.
2.7. Die Ableitung der Logarithmusfunktion
Wie üblich setzen wir an:
\$f'(x)=lim_{h->0} {ln(x+h)-ln(x)}/h\$,
wobei wir das 2. Logarithmusgesetz nutzen können und im Zähler \$ln(x+h)-ln(x)\$ als \$ln({x+h}/x)=ln(1+h/x)\$ schreiben können.
Nun ersetzen wir, wie bei der Herleitung der Ableitung der e-Funktion, alle \$h\$ durch \$1/n\$ und lassen das \$n->oo\$ laufen, anstatt das \$h->0\$. Somit erhält man
\$f'(x)=lim_{n->oo} ln(1+1/{n*x})/{1/n}\$.
Anstatt durch \$1/n\$ zu dividieren kann man den Zähler auch mit \$n\$ multiplizieren, so dass man den Term
\$lim_{n->oo} n*ln(1+1/{n*x})\$
erhält. Mit dem 3. Logarithmusgesetz erhält man
\$lim_{n->oo} ln((1+1/{n*x})^n)=lim_{n->oo} ln((1+{1/x}/n)^n)\$.
Da der ln selbst mit dem \$n\$ nichts zu tun hat, kann man den Limes in den ln ziehen und erhält als Ausdruck
\$ln(lim_{n->oo}(1+{1/x}/n)^n)\$
Den inneren Teil kennen wir schon aus der Herleitung der Eulerschen Zahl. Dort wurde in der Vertiefung erwähnt, dass \$lim_{n->oo} (1+a/n)^{n}\$ gegen \$e^a\$ läuft. Bei uns entspricht das \$1/x\$ dem a, so dass der Ausdruck im ln für \$n->oo\$ gegen \$e^{1/x}\$ läuft. Also bleibt übrig:
\$f'(x)=ln(e^{1/x})=1/x * ln(e)=1/x*1=1/x\$
Somit erhält man als überraschend einfaches Ergebnis für die
Ableitung der natürlichen Logarithmusfunktion:
Die Ableitung von \$f(x)=ln(x)\$ ist \$f'(x)=1/x\$.
Um beispielsweise die Ableitung von \$f(x)=ln(x^2)\$ zu bestimmen, könnte man unter Einsatz der Kettenregel so vorgehen:
\$f'(x)=1/{x^2} *2x={2x}/{x^2}=2/x\$
Alternative Herleitung ohne Differenzialquotient:
\$e^{ln(x)}=x\$ (Definition des ln)
Ableiten beider Seiten unter Anwendung der Kettenregel:
\$e^{ln(x)} * (ln(x))'=1\$
Jetzt \$e^{ln(x)}\$ wieder durch \$x\$ ersetzen:
\$x * (ln(x))'=1\$
und nach (ln(x))' auflösen:
\$(ln(x))'=1/x\$
3. Ableitung der allgemeinen Exponentialfunktion
Im Kapitel über die e-Funktion war als Eingangsaufgabe die Ableitung von \$g(x)=2^x\$ zu bilden. Mit den Erkenntnissen aus diesem Kapitel ist es nun auch möglich, diese Aufgabe zu lösen. Zunächst formen wir den Term so um, dass die e-Funktion ins Spiel kommt:
\$g(x)=2^x=(e^{ln(2)})^x\$
Diese Umformung stimmt, da \$e^{ln(2)}=2\$ ist. Mit dem Potenzgesetz \$(a^b)^c=a^{b*c}\$ kann man den Term noch umschreiben zu:
\$g(x)=e^{ln(2)*x}\$
und diesen kann man mit Hilfe der Kettenregel ableiten zu
\$g'(x)=e^{ln(2)*x}*ln(2)=2^x*ln(2)\$,
womit die Aufgabe gelöst ist. Allgemein kann man formulieren:
Ableitung einer Exponentialfunktion:
Die Ableitung einer Exponentialfunktion der Form
\$f(x)=a^x\$
mit \$a>0\$ lautet
\$f'(x)=a^x * ln(a)=f(x)*ln(a)\$.